CharlieT, was there any evidence that the weight of the guns was re-evaluated (reduced) after the King increased the number of guns from 90 to a maximum of 102?
17th Century Ship Design and the Sovereign of the Seas (1637)
Perhaps not ten times the value of a standard two decker, but I believe it was said that two or perhaps three standard vessels could have been built for the cost of SotS. The carvings certainly blew the budget out of the water, so to speak.
Darivs
No, there is isn't any evidence that I am aware of that suggests the weight of the guns was re-evaluated. The additional guns, while still heavy, were among the lightest guns on this ship. More importantly, the biggest concern would have been the weight at the stern. The ship was already heavy here due to the weight of the aft upper decks and the weight of the stern chase guns. Putting more weight here could have caused the stern chase ports to go under water. Pett avoided this potential disaster by putting the additional guns elsewhere. He them along both the forecastle and half deck. This placement also helped to distribute their weight. Finally, these were decks that were already carrying guns and, therefore, had beams strong enough to support their weight. What Pett did clearly worked. The ship didn't sink.
No, there is isn't any evidence that I am aware of that suggests the weight of the guns was re-evaluated. The additional guns, while still heavy, were among the lightest guns on this ship. More importantly, the biggest concern would have been the weight at the stern. The ship was already heavy here due to the weight of the aft upper decks and the weight of the stern chase guns. Putting more weight here could have caused the stern chase ports to go under water. Pett avoided this potential disaster by putting the additional guns elsewhere. He them along both the forecastle and half deck. This placement also helped to distribute their weight. Finally, these were decks that were already carrying guns and, therefore, had beams strong enough to support their weight. What Pett did clearly worked. The ship didn't sink.
Last edited:
This next section is a bit on the long side, so I will divide it into chewable chunks by dividing it into two posts. I'll post the second part later this week. The reference list for both posts will be in this second part. Yes, we will get to the Sovereign but, to my mind at least, its important to put some context around this ship.
Introduction (continued)
Ship design was just beginning its journey towards modernization when the Sovereign was built. Some shipwrights were now taking the radical step of drawing plans of their ships before they built them. This was a big step away from the previous tradition of applying a set of proportional rules that they had memorized.
Proportional rules, which varied among shipwrights, gave the dimension of one part of a ship as a proportion of another part. Dimensions were often computed from a ship’s widest part (e.g., “the floor must never be more than ⅕ nor less that ¼ of the breadth”), though the keel’s length and a ship’s depth were also used. Even these three dimensions could be expressed as a proportion of another of them.[1] Nevertheless, the practice of starting with all three of them was common because the shipwright and whoever was commissioning the ship usually came to agree upon them before construction began. Proportional rules persisted from quite some time, though in later times they were written. These written rules are seen in works like the Treatise on Shipbuilding and Sir Anthony Deane’s Doctrine of Naval Architecture.
Because so little was written down, a ship’s frames were shaped in the shipyard, and not on drafting table. This meant that ship design and construction were not separate endeavors. (Johnston 1994, pgs 119-120) :The lack of drawn plans also affected how ship design was taught and learned. The primary way shipwrights could teach was by providing examples, and the primary way that their apprentices could learn was by observing and copying those examples. This kind of instruction was delivered informally, and given as directions and advice to be followed on the job. (Johnston 1994, pg 126)
Sometimes, models of ships were also built, but they may not have played much of a role in ship design. China may have been an exception. Models built by the Song Dynasty (960 – 1279) sought to standardize ship types by preparing a set of scale models that were sent to various shipyards with instructions for how to build a ship. On the other hand, models built in the time of the Egyptian pharaohs may have been votive, a 1606 model of the Venetian galley Bucintoro was probably made for decoration, and Peter Pett’s model of the Sovereign of the Seas (Peter was this ship’s builder.[2]) was not used to build the Sovereign; His father, Phineas Pett, drew plans for this ship. Pett’s model is worth some comment A visitor to Peter Pett’s house described a model “of admirable workmanship, curiously painted and gilt, with azure and gold, so contrived that every timber in her might be seen, and left open and unplanked for that purpose”. This model, which did not have planking on the lower hull, may be the first example of a Navy Board-style model. (Ball and Stephens 2018, pg 16)
The British Navy Board came to routinely request such models in 1650, though it is not clear why. Models took a long time to build, and were expensive. The more elaborate models may have been built while the ships they portrayed were also being built, and completed after the actual ship was. It is also unclear whether many of these models represent ships “as built.” Models were too fragile to carry around a shipyard, and their frames could not be taken apart to make measurements. Instead of being design templates, these models probably served to help naval administrators better understand ship design and construction. (Ferriero 2007, pgs 38-40, and 42) The realm of actual design lay in drawn plans.
The earliest known ship plans appear in treatises. (Ferriero 2007, pg 40) The earliest surviving “treatise” is contained in a book[3] written in about 1434 by Michael of Rhodes, who was a member of the Venetian navy for over 40 years. (Dibner Inst. History Sci. Technology, Micheal of Rhodes 2005) Michael’s text contains a series of proportional rules that compute a ship’s principal dimensions from the length of the keel. His work is about how to build a standard galley that has already been designed, and not about how to design one from scratch. All galleys were built by the Venetian government in its own shipyard. Since they were expensive to build, and were financed using the public's money, it is not surprising that government officials wanted to know what it was that ship builders were building, and wanted make sure they were building the best ships for the money. As such, the context for Michael’s approach was bureaucratic. (Dibner Inst. History Sci. Technology, Ships and Shipbuilding: Design and Construction 2005) This was not unique. Ship plans in many countries appear to have become popular for bureaucratic reasons. Plans offered administrators a way to standardize and control shipbuilding by giving shipbuilders an inexpensive template to follow. (Ferriero 2007, pg 42)
Ship design in most of the rest of Europe was not as advanced as Venice. It was over a century before the idea of planning a ship on paper was introduced in England. Matthew Baker (1530-1613), who was likely influenced by the Venetian way of doing things, appears to be responsible for this. A possible source for Baker’s awareness of Venetian practice is suggested by navy quarterly accounts, where Baker’s name appears directly above that of Augustino Levello. Levello was a Venetian shipwright who originally brought to England to build galleys for Henry Vlll, but who remained in English service for over 40 years. Baker learned and adapted not just Venetian graphic techniques, but even adopted their terminology. (Johnston 1994, pg 128)
Matthew Baker was familiar with the shipyard since his childhood. His father, James Baker, designed ships for Henry VIII, and is credited as being the first to come up with the idea of cutting holes in a ship’s sides so that guns could be placed on its lower decks. (Blatcher 1989) (McKittrick 2018, pg 271) Matthew, with one or two others, was responsible for building many of the ships that fought the Spanish Armada in 1588. (Johnston 1994, pg 107)
When Matthew introduced the idea of designing ships on paper, the time was ripe for it. Global exploration, the desire for trade with other nations, and the desire to put more guns on ships created a need for bigger ships. Partly as a result of this, and partly because holes were now being cut in a ship’s side, English ship construction was changing from a “shell first” method of construction to carvel construction. In “shell first” construction, ships are built clinker style, like some of the smaller boats seen today. In this construction method, the keel, stem, and sternpost are laid first, and the hull is then built up as a shell of overlapping planks that run from stem to stern. Frames to strengthen the hull are added afterwards. (Johnston 1994, pg 120)
In carvel construction, English naval vessels, like earlier Mediterranean and Iberian ships, were “skeleton-built.” As with “shell first” construction; the keel stem and sternposts were erected first. Next, however, the ship’s frames were attached along the length of the keel, and before the ship planked. (Johnston 1994, pg 120) Although the judgment by eye inherent in clinker construction had often proved imperfect before, its deficiencies were highlighted by the need to have an accurate pattern of frames on a scale large enough to produce an ocean-going vessel, (Blatcher 1989) and to reliably accommodate gun ports.
Baker’s carvel-type construction practices are described in his Fragments of Ancient English Shipwrightry. The name was given to Baker’s works by Samuel Pepys, who eventually became Chief Secretary to the Admiralty despite his lack of maritime experience. Pepys’s choice of title is appropriate. Fragments is not a coherent volume; its format and style vary considerably throughout. (Johnston 1994, pg 117) It is a collection of miscellaneous notes and incomplete plans of ships that Baker began to compile somewhere around 1580, and that was continued by one of his apprentices, John Wells (Castro 2002). Wells was the storekeeper at the Depford ship yards, and mathematically knowledgeable. He assisted in constructing logarithmic tables soon after John Napier discovered them. (Johnston 1994, pg 163)
Baker not only put his plans on paper, he also used mathematics to design his ships. As shown by later 17th century works, Baker’s mathematical approach led to even more sophisticated methods. These methods used geometry and trigonometry (algebra was involved in using both). These subjects, in addition to more advanced courses,) are now offered in the typical American high school. In the Baker’s time, and in the early 17th century, they were “cutting edge.”
“Cutting edge” mathematics would not have been easy for most 17th century shipwrights. Most were innumerate, and struggled with simple addition and subtraction. Indeed, use of mathematical techniques for designing ships was likely confined to a handful of elite shipwrights.
Only a few ever received training in how to design a ship. Edward Bushnell complained that these were only the most favored apprentices. As a result, until 1645, designing ships was almost exclusively conducted by Master Shipwrights of the Dockyards, and the Surveyor of the Navy who came from their ranks. To reach their positions, shipwrights served a seven-year apprenticeship under either a qualified shipwright or a dockyard officer, and required the patronage of a senior dockyard officer for advancement. This encouraged a self-perpetuating hierarchy. (Hemingway 2002, pg 26) Many shipwrights spent time at sea as ship's carpenters, though few of those who reached the higher ranks of the profession did so. (Hemingway 2002, pg 21)
One of these elite shipwrights was Phineas Pett, designer of the Sovereign of the Seas (1637). In his autobiography, Pett writes of time he spent with Baker in the winter of 1505-1596 by saying “in the evenings, commonly I spent my time to good purposes, as in cyphering and drawing, and practising to attain the knowledge of my profession, and I then found Mr. Baker sometime forward to give me instructions, from whose help I must acknowledge I received my greatest lights.” (Perrin 1918, pg 7) A letter that Pett sent to Baker in April of 1603, Pett echoes this sentiment by saying “although I served no years in your service, yet I must ever acknowledge whatever I have of any art (if I have any) it came only from you. (Perrin 1918, pg lv)
[1] The Treatise on Shipbuilding tells us that the best proportion for the breadth is 7/3 the depth, and the best proportion for the breadth is 9/25 of the keel’s length.
[2] A 1637 brochure by Heywood noted that Pett made the model “before he was full five and twenty yeares of age.” (Heywood 1637) This implies the model was built in about 1630. Sephton suggests the model was conveyed to the King in 1634 (Sephton 2011, pg 28)
[3] The manuscript can be viewed at https://brunelleschi.imss.fi.it/michaelofrhodes/index.html.
Introduction (continued)
Early 17th Century Ship Design
The Sovereign was launched the same year the first opera house opened in Venice. The year before, the Puritans established Harvard University in the colony of Massachusetts. Four years before, Galileo arrived in Rome for his trial before the Inquisition. Descartes would publish his “Meditations on First Philosophy” only four years after its launch. Cardinal Richelieu of France reputedly created the table knife the year of this ship’s launch.Ship design was just beginning its journey towards modernization when the Sovereign was built. Some shipwrights were now taking the radical step of drawing plans of their ships before they built them. This was a big step away from the previous tradition of applying a set of proportional rules that they had memorized.
Proportional rules, which varied among shipwrights, gave the dimension of one part of a ship as a proportion of another part. Dimensions were often computed from a ship’s widest part (e.g., “the floor must never be more than ⅕ nor less that ¼ of the breadth”), though the keel’s length and a ship’s depth were also used. Even these three dimensions could be expressed as a proportion of another of them.[1] Nevertheless, the practice of starting with all three of them was common because the shipwright and whoever was commissioning the ship usually came to agree upon them before construction began. Proportional rules persisted from quite some time, though in later times they were written. These written rules are seen in works like the Treatise on Shipbuilding and Sir Anthony Deane’s Doctrine of Naval Architecture.
Because so little was written down, a ship’s frames were shaped in the shipyard, and not on drafting table. This meant that ship design and construction were not separate endeavors. (Johnston 1994, pgs 119-120) :The lack of drawn plans also affected how ship design was taught and learned. The primary way shipwrights could teach was by providing examples, and the primary way that their apprentices could learn was by observing and copying those examples. This kind of instruction was delivered informally, and given as directions and advice to be followed on the job. (Johnston 1994, pg 126)
Sometimes, models of ships were also built, but they may not have played much of a role in ship design. China may have been an exception. Models built by the Song Dynasty (960 – 1279) sought to standardize ship types by preparing a set of scale models that were sent to various shipyards with instructions for how to build a ship. On the other hand, models built in the time of the Egyptian pharaohs may have been votive, a 1606 model of the Venetian galley Bucintoro was probably made for decoration, and Peter Pett’s model of the Sovereign of the Seas (Peter was this ship’s builder.[2]) was not used to build the Sovereign; His father, Phineas Pett, drew plans for this ship. Pett’s model is worth some comment A visitor to Peter Pett’s house described a model “of admirable workmanship, curiously painted and gilt, with azure and gold, so contrived that every timber in her might be seen, and left open and unplanked for that purpose”. This model, which did not have planking on the lower hull, may be the first example of a Navy Board-style model. (Ball and Stephens 2018, pg 16)
The British Navy Board came to routinely request such models in 1650, though it is not clear why. Models took a long time to build, and were expensive. The more elaborate models may have been built while the ships they portrayed were also being built, and completed after the actual ship was. It is also unclear whether many of these models represent ships “as built.” Models were too fragile to carry around a shipyard, and their frames could not be taken apart to make measurements. Instead of being design templates, these models probably served to help naval administrators better understand ship design and construction. (Ferriero 2007, pgs 38-40, and 42) The realm of actual design lay in drawn plans.
The earliest known ship plans appear in treatises. (Ferriero 2007, pg 40) The earliest surviving “treatise” is contained in a book[3] written in about 1434 by Michael of Rhodes, who was a member of the Venetian navy for over 40 years. (Dibner Inst. History Sci. Technology, Micheal of Rhodes 2005) Michael’s text contains a series of proportional rules that compute a ship’s principal dimensions from the length of the keel. His work is about how to build a standard galley that has already been designed, and not about how to design one from scratch. All galleys were built by the Venetian government in its own shipyard. Since they were expensive to build, and were financed using the public's money, it is not surprising that government officials wanted to know what it was that ship builders were building, and wanted make sure they were building the best ships for the money. As such, the context for Michael’s approach was bureaucratic. (Dibner Inst. History Sci. Technology, Ships and Shipbuilding: Design and Construction 2005) This was not unique. Ship plans in many countries appear to have become popular for bureaucratic reasons. Plans offered administrators a way to standardize and control shipbuilding by giving shipbuilders an inexpensive template to follow. (Ferriero 2007, pg 42)
Ship design in most of the rest of Europe was not as advanced as Venice. It was over a century before the idea of planning a ship on paper was introduced in England. Matthew Baker (1530-1613), who was likely influenced by the Venetian way of doing things, appears to be responsible for this. A possible source for Baker’s awareness of Venetian practice is suggested by navy quarterly accounts, where Baker’s name appears directly above that of Augustino Levello. Levello was a Venetian shipwright who originally brought to England to build galleys for Henry Vlll, but who remained in English service for over 40 years. Baker learned and adapted not just Venetian graphic techniques, but even adopted their terminology. (Johnston 1994, pg 128)
Matthew Baker was familiar with the shipyard since his childhood. His father, James Baker, designed ships for Henry VIII, and is credited as being the first to come up with the idea of cutting holes in a ship’s sides so that guns could be placed on its lower decks. (Blatcher 1989) (McKittrick 2018, pg 271) Matthew, with one or two others, was responsible for building many of the ships that fought the Spanish Armada in 1588. (Johnston 1994, pg 107)
When Matthew introduced the idea of designing ships on paper, the time was ripe for it. Global exploration, the desire for trade with other nations, and the desire to put more guns on ships created a need for bigger ships. Partly as a result of this, and partly because holes were now being cut in a ship’s side, English ship construction was changing from a “shell first” method of construction to carvel construction. In “shell first” construction, ships are built clinker style, like some of the smaller boats seen today. In this construction method, the keel, stem, and sternpost are laid first, and the hull is then built up as a shell of overlapping planks that run from stem to stern. Frames to strengthen the hull are added afterwards. (Johnston 1994, pg 120)
In carvel construction, English naval vessels, like earlier Mediterranean and Iberian ships, were “skeleton-built.” As with “shell first” construction; the keel stem and sternposts were erected first. Next, however, the ship’s frames were attached along the length of the keel, and before the ship planked. (Johnston 1994, pg 120) Although the judgment by eye inherent in clinker construction had often proved imperfect before, its deficiencies were highlighted by the need to have an accurate pattern of frames on a scale large enough to produce an ocean-going vessel, (Blatcher 1989) and to reliably accommodate gun ports.
Baker’s carvel-type construction practices are described in his Fragments of Ancient English Shipwrightry. The name was given to Baker’s works by Samuel Pepys, who eventually became Chief Secretary to the Admiralty despite his lack of maritime experience. Pepys’s choice of title is appropriate. Fragments is not a coherent volume; its format and style vary considerably throughout. (Johnston 1994, pg 117) It is a collection of miscellaneous notes and incomplete plans of ships that Baker began to compile somewhere around 1580, and that was continued by one of his apprentices, John Wells (Castro 2002). Wells was the storekeeper at the Depford ship yards, and mathematically knowledgeable. He assisted in constructing logarithmic tables soon after John Napier discovered them. (Johnston 1994, pg 163)
Baker not only put his plans on paper, he also used mathematics to design his ships. As shown by later 17th century works, Baker’s mathematical approach led to even more sophisticated methods. These methods used geometry and trigonometry (algebra was involved in using both). These subjects, in addition to more advanced courses,) are now offered in the typical American high school. In the Baker’s time, and in the early 17th century, they were “cutting edge.”
“Cutting edge” mathematics would not have been easy for most 17th century shipwrights. Most were innumerate, and struggled with simple addition and subtraction. Indeed, use of mathematical techniques for designing ships was likely confined to a handful of elite shipwrights.
Only a few ever received training in how to design a ship. Edward Bushnell complained that these were only the most favored apprentices. As a result, until 1645, designing ships was almost exclusively conducted by Master Shipwrights of the Dockyards, and the Surveyor of the Navy who came from their ranks. To reach their positions, shipwrights served a seven-year apprenticeship under either a qualified shipwright or a dockyard officer, and required the patronage of a senior dockyard officer for advancement. This encouraged a self-perpetuating hierarchy. (Hemingway 2002, pg 26) Many shipwrights spent time at sea as ship's carpenters, though few of those who reached the higher ranks of the profession did so. (Hemingway 2002, pg 21)
One of these elite shipwrights was Phineas Pett, designer of the Sovereign of the Seas (1637). In his autobiography, Pett writes of time he spent with Baker in the winter of 1505-1596 by saying “in the evenings, commonly I spent my time to good purposes, as in cyphering and drawing, and practising to attain the knowledge of my profession, and I then found Mr. Baker sometime forward to give me instructions, from whose help I must acknowledge I received my greatest lights.” (Perrin 1918, pg 7) A letter that Pett sent to Baker in April of 1603, Pett echoes this sentiment by saying “although I served no years in your service, yet I must ever acknowledge whatever I have of any art (if I have any) it came only from you. (Perrin 1918, pg lv)
[1] The Treatise on Shipbuilding tells us that the best proportion for the breadth is 7/3 the depth, and the best proportion for the breadth is 9/25 of the keel’s length.
[2] A 1637 brochure by Heywood noted that Pett made the model “before he was full five and twenty yeares of age.” (Heywood 1637) This implies the model was built in about 1630. Sephton suggests the model was conveyed to the King in 1634 (Sephton 2011, pg 28)
[3] The manuscript can be viewed at https://brunelleschi.imss.fi.it/michaelofrhodes/index.html.
I really love this thread. Thank you, CharlieT!
Great information. Thanks.
Bill
Bill
All things 17th C., are readily received on this forum. Fascinating research!
ALSO RESEARCH DONE BY WALDAMER FASINATI9NG RESEARCH DUTCH, FRENCHY ETC RESEARCH CHECK IT OUT . GOD BLES STAY SAFE AQLL DON
Hi Charlie,
I find this information very interesting and informative. I will be looking forward to your posts. Thanks for sharing your work with us.
Bill
I find this information very interesting and informative. I will be looking forward to your posts. Thanks for sharing your work with us.
Bill
This post completes the section on early 17th century ship design.
Baker emphasizes its importance by explaining what happened when shipwrights did not know mathematics. He writes:
“For as mich as the goodnis of everi shipp doth consist in the parfitnes of the midship mold it is requerid the same be parfitly made all thoug at this day sum ther be that ueseth Jeometricall demonstration for the same it such as ar unparfit and they not abell to render a reason therof for that the want the ij [two][1] soporting pilars of everi art ...”
Here, he is saying that good ships require good midship bends, and too many shipwrights of his era lacked the knowledge of arithmetic and geometry (“the two supporting pillars of every art”) necessary to determine their shapes. (Blatcher 1989)
Baker is not alone in complaining about how lack of mathematical prowess among shipwrights led to defective ships. George Waymouth, probably in the early 17th century, wrote;
“The Shipwrights of England and of Christendom build ships only by uncertain traditional precepts and observations and chiefly by the deceiving aim of their eye, where for want of skill to work by such proportions as in Art is required and is ever certain, I have found these defects.” (Perrin 1918, pg lxxii)
The Treatise on Shipbuilding (ca 1620-1625; hereafter referred to as the Treatise) chimes in by saying that “so many times good ships are spoiled in the building whose principal lines were well contrived in the plotting. The chiefest reason is want of skill in Arithmetic and Geometry…”
By the mid 17th century, mathematics had become so engrained in ship design that the shipwright Edmund Bushnell concluded that drawn plans might not be needed at all. The important dimensions of a ship could be determined using math;
“ for in this kind of Arithmetical Work, it mattereth not, whether there be any Draught drawn at all, or no, if the builder only note in his Book the length by the Keel, and the breadth at the Beam, the Rack [rake] of the Stem, Rack of the Post, depth of the Water to Sail in depth of the Hould, height of the Waals abaft, afore at the Midships, and all the remarkable things to be noted, he may be able to Build a Vessel, and never draw a Draught at all, and yet affirm his Work to be absoluely true, according to Art, and a great deal more exact than by Draught…”. (Bushnell 1678, 30)
This is not as far-fetched as it sounds. The mathematical approach used to generate the present plans, and the dimensions provided herein, are sufficient to accomplish much of Bushnell’s goal. As a result, anyone attempting to construct a model from the present plans can build most of it from the provided dimensions. The drawn plans are largely superfluous.
Because mathematics was considered so important, nearly every major work on ship design written over the two centuries after Baker’s Fragments begins with one or more chapters about it (the Treatise is a notable exception). Initially, these works describe only geometry, which is understandable. It was a pillar of classical education, and was taught to all educated men. By the time of Mungo Murray’s 1754 Treatise on Ship-Building and Navigation (Murray 1754) and Steel’s 1805 The Shipwright’s Vade-Mecum,[2] these introductory sections also contained considerable information about trigonometry.
The importance of mathematics, at least among elite shipwrights., may be obscured by the lack of sophistication in some works from the early 17th century. They were, however, intended for different audiences. Edmund Bushnell’s 1664 treatise is geared to practicing shipwrights with little or no knowledge of how to use math to define the shape of a ship, though he repeatedly characterizes is work as “arithmetical.” As a work not intended for the elite, it keeps its subject simple. This is probably why Bushnell’s work was widely read. It was printed in five separate editions (the first was appeared in 1664, two editions appeared in 1669, and the remaining two in 1678 and 1688). Later, it was included almost word-for-word in three editions of another work called “Marine Architecture or, the Ship-Builder’s Assistant: Containing Directions for Carrying on a Ship, from the first laying of the Keel, to the actual Going to Sea” that was published in 1736, 1739, and 1748. (Olaberria 2018, 83)
Sir Anthony Deane’s Doctrine of Naval Architecture was written for Samuel Pepys, a man not known for his knowledge of ship design, and who was Deane’s patron. Deane’s descriptions are incomplete, often vague, and he uses mathematics to form arcs so simple that they may be simplifications he made for the purpose of explanation (Endsor 2020, pgs 109, 110). Perhaps Deane’s intended audience explains why he appears more interested in letting us know how much he knows rather than telling us what he knows. His work also has a self-promotional air about it. No other contemporary work on naval architecture makes such liberal use of the first person singular. Edmund Bushnell’s work was into its third printing when Anthony Deane wrote his Doctrine in 1670.
Both Bushnell and Dean stand in contrast to the Treatise, whose author displays considerable mathematical skill. The Treatise may have been written for apprentice shipwrights, and it appears to describe the actual practice of ship design. (Endsor 2020, pg 112). If the Treatise was used to teach apprentices, it would be following a precedent set by Mathew Baker. His “Fragments” were written despite shipwright’s secrecy, and at least part of them seem to have been a teaching tool for his pupils and apprentices. (Johnston 1994, pg 132)
The identity of the Treatise’s author is unknown. We do not even have the original manuscript. All we have are copies that abruptly end by referring to a table that no longer exists. Salisbury suggests the author was the same John Wells, (Salisbury 1958),[3] who wrote some of the Fragments. This may explain why its proportions for a ship’s main dimensions and the sweeps of the midship bend agree almost word-for word with those on a quarto sheet pasted to the last page of the Fragments. (Salisbury 1958) Others have suggested that the Treatise’s author was Phineas Pett (Coates 1981), but the Treatise’s failure to mention 3-decked ships makes this unlikely.
Supporting the idea of the Treatise as a teaching aid is that it begins as like an introductory textbook. It starts with the definition of a ship:
“A ship is a concave body of framed timber, plank, and ironwork, and contrived into several decks and rooms fitted for the use of men, munition, and victuals.”
It continues its “introductory” text with definitions of what a ship’s hull is, and then provides several pages of additional definitions and descriptions, including definitions of planks, decks, knights, capstans, and more.
Thereafter, the Treatise becomes quite sophisticated for its time. It provides numbers that lie to the right of the decimal point. Many shipwrights of the Sovereign’s era were uncomfortable with this. They preferred to work with fractions. Deane is an example of this. He often uses fractions that are unusual to the modern eye. For example, for smaller ships, Deane says he uses a transom whose width is 20/27 of the breadth. The Treatise even uses logarithms.[4] The use of logarithms shows that the its author was someone who was aware of recent developments in mathematics. This lends credence to the idea that Wells, who was a mathematician, was its author.
The mathematics embodied in the Treatise and other works on ship design do not mean that shipbuilding had become a scientific process. When Deane or the Treatise, for example, recommend a certain proportion, this proportion is still based on the experiences and prejudices of the builder (Lavery, Introduction 1982, pg 22), and not on empirically rigorous investigations of what worked best.
Nevertheless, ships of this era were the significant achievements. No other human constructions brought together mathematics, hydrodynamics (as seen in the understanding, however rudimentary, of the functions of rising and narrowing lines), an implicit physics that determined how thick ropes and blocks had to be to withstand whatever strain they would be put under, the astronomy required for using navigational instruments, the metallurgy required for gun founding, and more. The surprising thing is not what those who build ships and the devices aboard them did not know, it is what they did know.
Unfortunately, shipwrights do not always tell us what they knew. English shipwrights were particularly secretive about those aspects of ship design that affected how well a ship sailed. These aspects are described by the heights and curves of lines that describe where and how a ship narrows towards the bow and stern. They are called the rising and narrowing lines. The Treatise describes them by saying that:
“…the chief properties of a good ship … are 3: to go well, to steer well, and to bear a good sail. All [of][5] which depends upon the choice of lines for each several plane, for the rising lines must be neither too high nor too low, nor the narrowing lines to lank nor too full, nor the s[weeps] of the bends too round or too straight…”[6]
Because of the perceived importance and the secrecy of these lines, it is no wonder that a letter written by Sir Henry Sheers that refers to them as “mysterious lines.” (Endsor 2020) It is also no wonder that Edmund Bushnell complains about this secrecy in the introduction to his 1678 edition of “The Complete Ship-Wright.” (Bushnell 1678) His description of shipwrights tells us:
“their knowledge they desire to keep to themselves, or at least among so small a number as they can; for although some of them have many Servants, and by Indenture (I suppose) bound to teach them all alike the fame Art and Mysterie that he himself useth; yet it maybe he may teach some one, and the rest must be kept ignorant: so that those Ship-wrights, although bred by such knowing Men yet they are able to teach their Servants nothing more than to Hew, or Dub ,to Fay a Piece when it is Moulded to his place assigned, or the like: but if occasion require, that the greatest part of these Men, by being Carpenters of Ships, or the like, may be removed from England to Virginia, or New-England or the like Countreys, where Timber is plenty for their use, yet through their ignorance, they durst not undertake such a Work…”
This desire for secrecy even surfaces in contemporary works on naval architecture. Deane is certainly less than transparent in his descriptions. For example, when it comes to designing the all-important shape of the hull, he progressively reduces the radii of the arcs he uses used to draw the bends on his body plan, but does not even admit to doing so, let alone tell us how he does it. (Lavery, Deane's System 1670, pg 26)
Phineas Pett, and the entire Pett family of shipwrights, was no exception. It has been said of them that “this family furnished a succession of architects for the Royal Navy, their plans and methods being transmitted to one another with the profound secrecy then jealously maintained in the profession to which they belonged.” (Ford 1906) This is exemplified by Peter Pett’s comment after the Dutch sailed up the Thames Rive in 1667, and then on to the Chatham dockyard on the Medway, where they burned or captured fourteen English ships, one which was the English’ fleet’s flagship, the Royal Charles. Pett suggested that it was better that the Dutch had captured actual ships than his models for, if they had captured the latter, the secrets of his designs would have been revealed. (Lavery, The Ship of the Line 1984, pg 14)
The English crown also had an interest in keeping its country’s shipbuilding methods secret. It gave them naval superiority. Accordingly, the letter from Mansell, Pennington, Wells, and Pett that accompanied the listing of the Sovereign of the Sea’s dimensions says:
“Your Maty will be pleased to be informed that after mature debate we have likewise agreed upon the rules to be proportioned to each sweep of the midship bend, and where the bend is to be placed, and likewise of the rules to be held in her narrowing and rising lines, which we all pray may be only imparted to your Maty.” [italics added]
France sent spies to several European countries to overcome this secrecy. They were usually arranged as visits through official channels with foreign governments. One such agent was sent to the Depford shipyards in England in 1663, and another agent travelled to England in 1671. The agents concluded that the hull proportions and masting of British warships were superior to those of the French. (Ferriero 2007, pg 64)
Exactly which ships these agents examined is unknown, so the degree to which this superiority extended to ships with spritsail topmasts (these are ships, like the Sovereign, with a mast on the bowsprit) requires speculation. These early ships were unstable. Indeed, the presence of such a mast indicates instability. They achieved stability by relying on proper ballasting and on the sails’ trim. Today, stability is built in to ships. Almost every full-sized replica of a wooden ship has been modified to meet current standards of stability, sometimes because regulatory authorities would not allow a ship as unstable as the original to be built, and sometimes because builders did not want to sail in a ship that was so unstable. This highlights the notion that 17th century ships were designed and built by people who had very different notions of acceptable risk than we do, and who took very different things for granted. (Reid 2016)
Blatcher, Margaret. 1989. "Chatham Dockyard and a LIttle Known Shipwright, Matthew Baker (1530 -1613)." Archaeologia Cantiana (Kent Archeological Society) 107: 15-172.
Bushnell, Edmund. 1678. The Compleat Ship-Wright, Fourth Edition. London: William Fisher.
Castro, Filipe. 2002. Fragments of Ancient Shipwrightry. Texas A&M University Nautical Archaeology Program. Accessed January 6, 2021. https://nautarch.tamu.edu/shiplab/treatisefiles/ttfragments.htm.
Coates, J F. 1981. "The Authorship of a Manuscipt of Shipbuilding c 1600-1620." Mariner's Mirror, 67 285-286.
Dibner Inst. History Sci. Technology. 2005. Micheal of Rhodes. Accessed June 8, 2021. https://brunelleschi.imss.fi.it/michaelofrhodes/index.html.
—. 2005. Ships and Shipbuilding: Design and Construction. Accessed 1 11, 2022. https://brunelleschi.imss.fi.it/michaelofrhodes/ships_design.html.
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.
Ferriero, Larrie D. 2007. Ships and Science. Cambridge: Massachusetts Institute of Technology.
Ford, Thomas G. 1906. "Earliest English Navigation, and FIrst Schools of Warfare." Proceedings of The United States Naval Institute, 32 473-522.
Hemingway, James Peter. 2002. The Work of the Surveyors of the Navy during the Period of the Establishments: A Comparative Study of Naval Architeccture Between 1672 and 1755. Doctoral DIssertatioin, Bristol: University of Bristol.
Heywood, Thomas. 1637. "A True Description of His Majesties Royall Ship, Built this Yeare 1637 at Wooll-witch in Kent. To the great glory of the English Nation and not paraleld in the whole Christian Worl." London: John Oakes.
Johnston, S A. 1994. Making mathematical practice : gentlemen, practitioners and artisans in Elizabethan England (Doctoral thesis). https://doi.org/10.17863/CAM.19773.
Kirsch, Peter. 1988. The Galleon. London: Conway Maritime Press, Ltd.
Lavery, Brian. 1670. "Deane's System." In Deane's Doctrine of Naval Architecture, 1670, by Anthony Deane, 128. Annapolis, MD: Naval Institute Press.
Lavery, Brian. 1982. "Introduction." In Deane's Doctrine of Naval Architecture, 1670, 7-31. Annapolis: Naval Institute Press.
—. 1984. The Ship of the Line. Vols. Volume II: Design, Construction and FIttings. Londin: Conway Maritime Press.
McKittrick, Paul J. 2018. "Modernity and the Spirit of the Sea: Maritime Influences on Early Modern English State Institutions and Society, 1485-1763." Doctoral DIssertation. Georgia Institte of Technology, May.
Murray, Mungo. 1754. A Treatise on Ship-Building and Navigation. London: D. Henry and R. Cave.
Olaberria, Juan-Pablo. 2018. Ship Design Knowledge in Early Modern Europe: Royal Yachts and the Shared Knowedge of Ship-designers and Common Shipwrights. Vol. 1. 2 vols. Southampton: Doctoral Dissertation; University of Southampton.
Perrin, W G. 1918. The Autobiography of Phineas Pett. The Naval Records Society.
Reid, Phillip. 2016. "The Time Machine? Using Replica Analysis to Understand Merchant Ships and the Develmpment of the British Atlantic, 1600-1800." The Northern Mariner/Le marin du nord 26 (3): 299-316.
Salisbury, W. 1958. A Treatise on Shipbuilding. London: Society for Nautical Research, Occassional Publications No. 6.
Sephton, James. 2011. The Sovereign of the Seas. Stroud: Amberly Publishing.
[1] Throughout the present manuscript, brackets contain clarifications and corrections added to the original text.
[2] A vade mecum is a handbook or guide that is constantly kept at one’s side for consultation.
[3] A copy of the Treatise can be found in Peter Kirsch’s book “The Galleon.” (Kirsch 1988).
[4] The Treatise’s author uses logarithms to find the exact length of each sweep that makes up a bend. He does this because transforming the measurements from a small ship plan to the large, actual ship could result in substantial error. Logarithms are not discussed here because plans for model ship are often the same size, or nearly the same size as the model being built.
[5] Bracketed words within the quotes from the Treatise were added by Salisbury to increase its readability.
[6] This last sentence of this quote reveals some awareness of hydrodynamics as manifested in an understanding that the shape of the hull affected a ship’s handling and sailing ability.
Early 17th Century Ship Design (continued)
Matthew Baker’s idea to put plans on paper was in important technological advance for English shipwrights. Now, the results of mathematical calculations could be inexpensively and rapidly seen. The allowed shipwrights to experiment with different mathematical techniques. Without these techniques, progress would have been slow, had it occurred at all. None of the historically important wooden ships of the 17th through the 19th centuries would have been built the way they were. Maritime trade would have been vastly different, as would have been naval battles. Despite the importance of mathematics, it is almost never discussed in the popular literature on historic ships. Some shipwrights felt otherwise.Baker emphasizes its importance by explaining what happened when shipwrights did not know mathematics. He writes:
“For as mich as the goodnis of everi shipp doth consist in the parfitnes of the midship mold it is requerid the same be parfitly made all thoug at this day sum ther be that ueseth Jeometricall demonstration for the same it such as ar unparfit and they not abell to render a reason therof for that the want the ij [two][1] soporting pilars of everi art ...”
Here, he is saying that good ships require good midship bends, and too many shipwrights of his era lacked the knowledge of arithmetic and geometry (“the two supporting pillars of every art”) necessary to determine their shapes. (Blatcher 1989)
Baker is not alone in complaining about how lack of mathematical prowess among shipwrights led to defective ships. George Waymouth, probably in the early 17th century, wrote;
“The Shipwrights of England and of Christendom build ships only by uncertain traditional precepts and observations and chiefly by the deceiving aim of their eye, where for want of skill to work by such proportions as in Art is required and is ever certain, I have found these defects.” (Perrin 1918, pg lxxii)
The Treatise on Shipbuilding (ca 1620-1625; hereafter referred to as the Treatise) chimes in by saying that “so many times good ships are spoiled in the building whose principal lines were well contrived in the plotting. The chiefest reason is want of skill in Arithmetic and Geometry…”
By the mid 17th century, mathematics had become so engrained in ship design that the shipwright Edmund Bushnell concluded that drawn plans might not be needed at all. The important dimensions of a ship could be determined using math;
“ for in this kind of Arithmetical Work, it mattereth not, whether there be any Draught drawn at all, or no, if the builder only note in his Book the length by the Keel, and the breadth at the Beam, the Rack [rake] of the Stem, Rack of the Post, depth of the Water to Sail in depth of the Hould, height of the Waals abaft, afore at the Midships, and all the remarkable things to be noted, he may be able to Build a Vessel, and never draw a Draught at all, and yet affirm his Work to be absoluely true, according to Art, and a great deal more exact than by Draught…”. (Bushnell 1678, 30)
This is not as far-fetched as it sounds. The mathematical approach used to generate the present plans, and the dimensions provided herein, are sufficient to accomplish much of Bushnell’s goal. As a result, anyone attempting to construct a model from the present plans can build most of it from the provided dimensions. The drawn plans are largely superfluous.
Because mathematics was considered so important, nearly every major work on ship design written over the two centuries after Baker’s Fragments begins with one or more chapters about it (the Treatise is a notable exception). Initially, these works describe only geometry, which is understandable. It was a pillar of classical education, and was taught to all educated men. By the time of Mungo Murray’s 1754 Treatise on Ship-Building and Navigation (Murray 1754) and Steel’s 1805 The Shipwright’s Vade-Mecum,[2] these introductory sections also contained considerable information about trigonometry.
The importance of mathematics, at least among elite shipwrights., may be obscured by the lack of sophistication in some works from the early 17th century. They were, however, intended for different audiences. Edmund Bushnell’s 1664 treatise is geared to practicing shipwrights with little or no knowledge of how to use math to define the shape of a ship, though he repeatedly characterizes is work as “arithmetical.” As a work not intended for the elite, it keeps its subject simple. This is probably why Bushnell’s work was widely read. It was printed in five separate editions (the first was appeared in 1664, two editions appeared in 1669, and the remaining two in 1678 and 1688). Later, it was included almost word-for-word in three editions of another work called “Marine Architecture or, the Ship-Builder’s Assistant: Containing Directions for Carrying on a Ship, from the first laying of the Keel, to the actual Going to Sea” that was published in 1736, 1739, and 1748. (Olaberria 2018, 83)
Sir Anthony Deane’s Doctrine of Naval Architecture was written for Samuel Pepys, a man not known for his knowledge of ship design, and who was Deane’s patron. Deane’s descriptions are incomplete, often vague, and he uses mathematics to form arcs so simple that they may be simplifications he made for the purpose of explanation (Endsor 2020, pgs 109, 110). Perhaps Deane’s intended audience explains why he appears more interested in letting us know how much he knows rather than telling us what he knows. His work also has a self-promotional air about it. No other contemporary work on naval architecture makes such liberal use of the first person singular. Edmund Bushnell’s work was into its third printing when Anthony Deane wrote his Doctrine in 1670.
Both Bushnell and Dean stand in contrast to the Treatise, whose author displays considerable mathematical skill. The Treatise may have been written for apprentice shipwrights, and it appears to describe the actual practice of ship design. (Endsor 2020, pg 112). If the Treatise was used to teach apprentices, it would be following a precedent set by Mathew Baker. His “Fragments” were written despite shipwright’s secrecy, and at least part of them seem to have been a teaching tool for his pupils and apprentices. (Johnston 1994, pg 132)
The identity of the Treatise’s author is unknown. We do not even have the original manuscript. All we have are copies that abruptly end by referring to a table that no longer exists. Salisbury suggests the author was the same John Wells, (Salisbury 1958),[3] who wrote some of the Fragments. This may explain why its proportions for a ship’s main dimensions and the sweeps of the midship bend agree almost word-for word with those on a quarto sheet pasted to the last page of the Fragments. (Salisbury 1958) Others have suggested that the Treatise’s author was Phineas Pett (Coates 1981), but the Treatise’s failure to mention 3-decked ships makes this unlikely.
Supporting the idea of the Treatise as a teaching aid is that it begins as like an introductory textbook. It starts with the definition of a ship:
“A ship is a concave body of framed timber, plank, and ironwork, and contrived into several decks and rooms fitted for the use of men, munition, and victuals.”
It continues its “introductory” text with definitions of what a ship’s hull is, and then provides several pages of additional definitions and descriptions, including definitions of planks, decks, knights, capstans, and more.
Thereafter, the Treatise becomes quite sophisticated for its time. It provides numbers that lie to the right of the decimal point. Many shipwrights of the Sovereign’s era were uncomfortable with this. They preferred to work with fractions. Deane is an example of this. He often uses fractions that are unusual to the modern eye. For example, for smaller ships, Deane says he uses a transom whose width is 20/27 of the breadth. The Treatise even uses logarithms.[4] The use of logarithms shows that the its author was someone who was aware of recent developments in mathematics. This lends credence to the idea that Wells, who was a mathematician, was its author.
The mathematics embodied in the Treatise and other works on ship design do not mean that shipbuilding had become a scientific process. When Deane or the Treatise, for example, recommend a certain proportion, this proportion is still based on the experiences and prejudices of the builder (Lavery, Introduction 1982, pg 22), and not on empirically rigorous investigations of what worked best.
Nevertheless, ships of this era were the significant achievements. No other human constructions brought together mathematics, hydrodynamics (as seen in the understanding, however rudimentary, of the functions of rising and narrowing lines), an implicit physics that determined how thick ropes and blocks had to be to withstand whatever strain they would be put under, the astronomy required for using navigational instruments, the metallurgy required for gun founding, and more. The surprising thing is not what those who build ships and the devices aboard them did not know, it is what they did know.
Unfortunately, shipwrights do not always tell us what they knew. English shipwrights were particularly secretive about those aspects of ship design that affected how well a ship sailed. These aspects are described by the heights and curves of lines that describe where and how a ship narrows towards the bow and stern. They are called the rising and narrowing lines. The Treatise describes them by saying that:
“…the chief properties of a good ship … are 3: to go well, to steer well, and to bear a good sail. All [of][5] which depends upon the choice of lines for each several plane, for the rising lines must be neither too high nor too low, nor the narrowing lines to lank nor too full, nor the s[weeps] of the bends too round or too straight…”[6]
Because of the perceived importance and the secrecy of these lines, it is no wonder that a letter written by Sir Henry Sheers that refers to them as “mysterious lines.” (Endsor 2020) It is also no wonder that Edmund Bushnell complains about this secrecy in the introduction to his 1678 edition of “The Complete Ship-Wright.” (Bushnell 1678) His description of shipwrights tells us:
“their knowledge they desire to keep to themselves, or at least among so small a number as they can; for although some of them have many Servants, and by Indenture (I suppose) bound to teach them all alike the fame Art and Mysterie that he himself useth; yet it maybe he may teach some one, and the rest must be kept ignorant: so that those Ship-wrights, although bred by such knowing Men yet they are able to teach their Servants nothing more than to Hew, or Dub ,to Fay a Piece when it is Moulded to his place assigned, or the like: but if occasion require, that the greatest part of these Men, by being Carpenters of Ships, or the like, may be removed from England to Virginia, or New-England or the like Countreys, where Timber is plenty for their use, yet through their ignorance, they durst not undertake such a Work…”
This desire for secrecy even surfaces in contemporary works on naval architecture. Deane is certainly less than transparent in his descriptions. For example, when it comes to designing the all-important shape of the hull, he progressively reduces the radii of the arcs he uses used to draw the bends on his body plan, but does not even admit to doing so, let alone tell us how he does it. (Lavery, Deane's System 1670, pg 26)
Phineas Pett, and the entire Pett family of shipwrights, was no exception. It has been said of them that “this family furnished a succession of architects for the Royal Navy, their plans and methods being transmitted to one another with the profound secrecy then jealously maintained in the profession to which they belonged.” (Ford 1906) This is exemplified by Peter Pett’s comment after the Dutch sailed up the Thames Rive in 1667, and then on to the Chatham dockyard on the Medway, where they burned or captured fourteen English ships, one which was the English’ fleet’s flagship, the Royal Charles. Pett suggested that it was better that the Dutch had captured actual ships than his models for, if they had captured the latter, the secrets of his designs would have been revealed. (Lavery, The Ship of the Line 1984, pg 14)
The English crown also had an interest in keeping its country’s shipbuilding methods secret. It gave them naval superiority. Accordingly, the letter from Mansell, Pennington, Wells, and Pett that accompanied the listing of the Sovereign of the Sea’s dimensions says:
“Your Maty will be pleased to be informed that after mature debate we have likewise agreed upon the rules to be proportioned to each sweep of the midship bend, and where the bend is to be placed, and likewise of the rules to be held in her narrowing and rising lines, which we all pray may be only imparted to your Maty.” [italics added]
France sent spies to several European countries to overcome this secrecy. They were usually arranged as visits through official channels with foreign governments. One such agent was sent to the Depford shipyards in England in 1663, and another agent travelled to England in 1671. The agents concluded that the hull proportions and masting of British warships were superior to those of the French. (Ferriero 2007, pg 64)
Exactly which ships these agents examined is unknown, so the degree to which this superiority extended to ships with spritsail topmasts (these are ships, like the Sovereign, with a mast on the bowsprit) requires speculation. These early ships were unstable. Indeed, the presence of such a mast indicates instability. They achieved stability by relying on proper ballasting and on the sails’ trim. Today, stability is built in to ships. Almost every full-sized replica of a wooden ship has been modified to meet current standards of stability, sometimes because regulatory authorities would not allow a ship as unstable as the original to be built, and sometimes because builders did not want to sail in a ship that was so unstable. This highlights the notion that 17th century ships were designed and built by people who had very different notions of acceptable risk than we do, and who took very different things for granted. (Reid 2016)
References
Ball, Nick, and Simons Stephens. 2018. Navy Board Ship Models. Barnsley (UK): Seaforth Publishing.Blatcher, Margaret. 1989. "Chatham Dockyard and a LIttle Known Shipwright, Matthew Baker (1530 -1613)." Archaeologia Cantiana (Kent Archeological Society) 107: 15-172.
Bushnell, Edmund. 1678. The Compleat Ship-Wright, Fourth Edition. London: William Fisher.
Castro, Filipe. 2002. Fragments of Ancient Shipwrightry. Texas A&M University Nautical Archaeology Program. Accessed January 6, 2021. https://nautarch.tamu.edu/shiplab/treatisefiles/ttfragments.htm.
Coates, J F. 1981. "The Authorship of a Manuscipt of Shipbuilding c 1600-1620." Mariner's Mirror, 67 285-286.
Dibner Inst. History Sci. Technology. 2005. Micheal of Rhodes. Accessed June 8, 2021. https://brunelleschi.imss.fi.it/michaelofrhodes/index.html.
—. 2005. Ships and Shipbuilding: Design and Construction. Accessed 1 11, 2022. https://brunelleschi.imss.fi.it/michaelofrhodes/ships_design.html.
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.
Ferriero, Larrie D. 2007. Ships and Science. Cambridge: Massachusetts Institute of Technology.
Ford, Thomas G. 1906. "Earliest English Navigation, and FIrst Schools of Warfare." Proceedings of The United States Naval Institute, 32 473-522.
Hemingway, James Peter. 2002. The Work of the Surveyors of the Navy during the Period of the Establishments: A Comparative Study of Naval Architeccture Between 1672 and 1755. Doctoral DIssertatioin, Bristol: University of Bristol.
Heywood, Thomas. 1637. "A True Description of His Majesties Royall Ship, Built this Yeare 1637 at Wooll-witch in Kent. To the great glory of the English Nation and not paraleld in the whole Christian Worl." London: John Oakes.
Johnston, S A. 1994. Making mathematical practice : gentlemen, practitioners and artisans in Elizabethan England (Doctoral thesis). https://doi.org/10.17863/CAM.19773.
Kirsch, Peter. 1988. The Galleon. London: Conway Maritime Press, Ltd.
Lavery, Brian. 1670. "Deane's System." In Deane's Doctrine of Naval Architecture, 1670, by Anthony Deane, 128. Annapolis, MD: Naval Institute Press.
Lavery, Brian. 1982. "Introduction." In Deane's Doctrine of Naval Architecture, 1670, 7-31. Annapolis: Naval Institute Press.
—. 1984. The Ship of the Line. Vols. Volume II: Design, Construction and FIttings. Londin: Conway Maritime Press.
McKittrick, Paul J. 2018. "Modernity and the Spirit of the Sea: Maritime Influences on Early Modern English State Institutions and Society, 1485-1763." Doctoral DIssertation. Georgia Institte of Technology, May.
Murray, Mungo. 1754. A Treatise on Ship-Building and Navigation. London: D. Henry and R. Cave.
Olaberria, Juan-Pablo. 2018. Ship Design Knowledge in Early Modern Europe: Royal Yachts and the Shared Knowedge of Ship-designers and Common Shipwrights. Vol. 1. 2 vols. Southampton: Doctoral Dissertation; University of Southampton.
Perrin, W G. 1918. The Autobiography of Phineas Pett. The Naval Records Society.
Reid, Phillip. 2016. "The Time Machine? Using Replica Analysis to Understand Merchant Ships and the Develmpment of the British Atlantic, 1600-1800." The Northern Mariner/Le marin du nord 26 (3): 299-316.
Salisbury, W. 1958. A Treatise on Shipbuilding. London: Society for Nautical Research, Occassional Publications No. 6.
Sephton, James. 2011. The Sovereign of the Seas. Stroud: Amberly Publishing.
[1] Throughout the present manuscript, brackets contain clarifications and corrections added to the original text.
[2] A vade mecum is a handbook or guide that is constantly kept at one’s side for consultation.
[3] A copy of the Treatise can be found in Peter Kirsch’s book “The Galleon.” (Kirsch 1988).
[4] The Treatise’s author uses logarithms to find the exact length of each sweep that makes up a bend. He does this because transforming the measurements from a small ship plan to the large, actual ship could result in substantial error. Logarithms are not discussed here because plans for model ship are often the same size, or nearly the same size as the model being built.
[5] Bracketed words within the quotes from the Treatise were added by Salisbury to increase its readability.
[6] This last sentence of this quote reveals some awareness of hydrodynamics as manifested in an understanding that the shape of the hull affected a ship’s handling and sailing ability.
Last edited:
I found the bit about stability and the use of the sprit topsail as an indication of instability to be particularly interesting.
It would be very interesting to have the connection between stability and sprit topsail explained.
Alvb
Agree with you there. You would expect the spritsail is used to stear around the vertical center axis of the ship together with its lateen sail.
The ships stability and center frame construction has an impact at the stabilty around the horizontal longitudal axis.
Secondly Dutch ships who had a boxy frame still had a sprit sail.
Background (continued)
Whole Molding and the Midship Bend
This section presents a simplified discussion of whole molding, and of drawing the midship bend. Its primary purpose is to introduce terms and concepts that will be used in later sections. More details will be presented later, in the appropriate places.Ships of the Sovereign’s era were built using a method called “whole molding.” In whole molding, the shapes of all a ship’s frames are derived from a master frame called the “midship bend.” A “bend” is every third or fourth of a ship’s frames. (Endsor 2020, 199) They are what shipwrights drew bends on their plans instead of frames. Deane tells us that bends are “just the distances of or spaces of every third timber to stand on the keel, and about a century later Mungo Murray explained; “… it is usual in draughts to lay down only every third or fourth timber….” (Murray 1754, 166) Because the shape of all of the other bends depended on the midship bend, none of them could be drawn on plans or built on ships until the midship bend’s shape was known. Shipwrights therefore determined its shape early in the planning process.
Despite its name, the midship bend did not always lie at the ship’s middle. The Newton Manuscript tells us that it “must never be placed abath [abaft] the midst of the keel nor never before ye ¼ thereof.” The Treatise tells us that it lies aft of the keel’s fore end by a distance equal to ⅓ of the keel’s total length, which is where it is on the current plans. The midship bend is often described as being the broadest frame on a ship, but this is not quite accurate. The frames surrounding it were equally broad. It is more precise to say that none of ship’s frames is broader than the midship bend.
We need only say for our present purposes that drawing the midship bend consists of drawing in a straight line for the ship’s floor, and then forming the bend’s outline by drawing several sweeps (i.e., arcs that are parts of circles; see Figure 1) though, often, the uppermost “sweep” was drawn as a straight line. The number of sweeps varied. Baker’s Fragments show bends with three or four sweeps, Bushnell uses three, the Treatise’s author draws four sweeps, and Deane uses five. Figure 1 shows a midship bend that has four sweeps. Moving upwards, they are called the sweep of the wrong head (Phineas Pett’s spelling for this term “runghead”), the futtock sweep (also called the reconciling sweep), the sweep of the breadth, and the hollowing sweep (also called the toptimber sweep). When three sweeps were used, a single arc was substituted for the futtock sweep and the sweep of the breadth. When five sweeps were used, a sweep called the sweep below the breadth began at the futtock sweep and ended at the bends’ greatest breadth, and a sweep called the sweep above the breadth was interposed between the greatest breadth and the hollowing sweep.
The completed plan for a bend did not consider the thickness of the planking that was attached to it. Another way to say this is that this drawing portrayed the molded beam, not the extreme beam.
The sweeps of the midship bend were drawn using radii computed from specific proportional rules. When these computations were complete, all that remained for the shipwright to do was put one leg of his compass in the appropriate places, and draw the sweeps with the other leg. Sir Anthony Deane, in his 1670 Doctrine offered a helpful way to do this neatly:
“And by the way I must tell you, for your more curious drawing without blemish, draw all your whole draught in every line with black lead, and then when you have done, you may ink it all together, and then rub all over the draught with a crumb of white bread and it will take out all the black lead, and by this means the draught will be very clean, and complete as you desire.”[1]
Using bread as an eraser was common. It could also help keep secrets. Thomas Miller told readers to conceal their rigging by drawing its lines in pencil, making prick marks at the ends of the yards, and then “with crums of white bread and a clean linen cloth I rub them out again … that you may easier draw them again if you have the occasion.” (Endsor 2020, 109)
Figure 1. The Sweeps of a Midship Bend
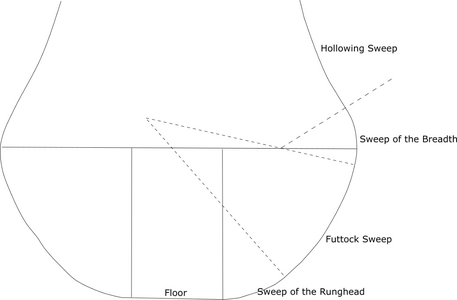
Note: The vertical lines indicate the floor’s lateral edges. The dashed lines that intersect the bend’s outline show the boundaries of the sweeps. The figure and the explanation of it in the text has been simplified for the present discussion.
The remaining frames were constructed after the midship bend had been finalized. This involved changing them in a way that allowed the midship bend to be used as a pattern. Initially, this consisted of using the radii of the midship bend’s sweeps for all the frames, and making them smaller and higher as they moved away from the midship bend. The upwards movement of the frames was given by a line called the rising line of the floor. This line showed how far above the keel the frame’s bottoms were. The height of each frame’s maximum breadth which was given by another rising line, was parallel to this line. Narrowing lines that corresponded to the rising lines were used to make the frames smaller. These lines described how a ship narrowed towards the bow and stern. (Lavery, Introduction 1982, 23)[2]
There were several problems with this early method of whole molding. It did not tell shipwrights how to construct the frames at the bow and stern, it did not produce a smooth hull, and it was incompatible with the heavier armament that was coming into use in the 1500’s. Its primary problem was that at the bow, the rising line of the floor had to rise steeply upwards to prevent the ship from being too blunt here. Since the rising line of the breadth was parallel to that of the floor, this increase led to a steep increase in the height of the frames’ maximum breadths. The decks followed the breadth, and no deck could be made this steep. Therefore, a break was put in the decks at the bow and stern, and the deck was abruptly raised. (Lavery, The Ship of the Line 1984, 13)
The need for a break in the deck was overcome by no later than 1586, when a second version of whole molding was introduced. (Lavery, The Ship of the Line 1984, 13) This version made the height of the breadth independent of the rising line of the floor. This allowed the breadth to stay flatter and lower, which eliminated the need to raise the decks. This is the method described in the Treatise. It retained the practice of using the radii of the sweeps at the midship bend for all of the frames. It thereby retained another difficulty inherent in the first version of whole molding; using the midship bend’s relatively large sweep of the breadth at the stern made it difficult to join the futtock sweep with it. The meant the breadth had to be kept narrow here, and it is partly why 17th century ships have such narrow sterns. (Lavery, The Ship of the Line 1984, 13), The lack of clear instructions for making the frames at the bow and stern also remained, as did the inability to produce a smooth hull. (Lavery, The Ship of the Line 1984, 13)
The second version of whole molding gave way to a new method for designing ships later in the 17th century. It addressed the need to keep the stern narrow by allowing the radius of the sweep of the breadth to decrease as the frames approached the stern. This meant that a ship could be kept broader here. The radii of the other sweeps were also allowed change as the frames move away from the midship bend. This method was used by Deane. It is evident in his drawings, though he never actually says he is reducing the sweeps’ radii, much less explain how he did it. (Lavery, The Ship of the Line 1984, 13) The lack of information on how Deane reduced the radii makes it impossible to faithfully use his system to draw the bends. We can only follow the simplified information given in his text. This text implies the radii are constant, and he gives formulae for them. Deane’s actual system is not whole molding in the traditional sense. Since the sweeps’ radii change, the midship bend cannot be used as a pattern for all the frames.
References
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.Lavery, Brian. 1982. "Introduction." In Deane's Doctrine of Naval Architecture, 1670, 7-31. Annapolis: Naval Institute Press.
—. 1984. The Ship of the Line. Vols. Volume II: Design, Construction and FIttings. Londin: Conway Maritime Press.
Murray, Mungo. 1754. A Treatise on Ship-Building and Navigation. London: D. Henry and R. Cave.
[1] A recipe for 17th century bread appears in Gervase Markham’s cookbook that was first published in London in 1615. This book, “The English Huswife, Containing the Inward and Outward Virtues Which Ought to Be in a Complete Woman,” tells us to “Take 3 quart of a pound of fine searced flowr: 2 spoonefulls of new barme worke this together wth hotte licore and cover yt close and let it stand and rest one houre & yt wilbe risen enough, then worke yt & breake yt well make small loaves & sett into the hotte oven the space of halfe an hour or lesse.” Searced flour is finely sifted and bolted flour. Barne is beer yeast. Since wheat as coarse as that used in the 17th century is not available now, the recipe works best if you mill home-grown wheat.
[2] We will have a lot more to say about the rising and narrowing lines later on. For the present purposes, we can think of the rising lines as lines drawn on a view of the ship’s profile (i.e., the sheer plan) and the narrowing lines as lines drawn on a view of the ships top (i.e., the half breadth plan) at elevations that correspond to the rising lines.
- Joined
- Jan 17, 2020
- Messages
- 20
- Points
- 58
Hello, I like to mention two more relevant sources:
Keltridge, in His Book (c.1675) provides a list of scantlings and lists the sweep radii for both a midship bend and another - stern bend. Here the radii for the lower and upper breadth sweeps are smaller than in the midship bend. Under the stern bend he lists the sweep for the hollow and the sweep for the hollow mould. So this indicates the idea of diminishing radii numerically (Deane only shows that only graphically) and also shows that some parts of bends are not used along the complete length of a hull.
A second, more early, source is a so called RINA or Scott manuscript, which unfortunately has been sold several years ago and is not available to read. Before that Michel Daeffler had been able to use for his book "Formes de carène et navires de combat : L'invention du vaisseau de ligne en Angleterre (1560-1642)". I wonder does anybody here have an access to a copy of this MS?
Keltridge, in His Book (c.1675) provides a list of scantlings and lists the sweep radii for both a midship bend and another - stern bend. Here the radii for the lower and upper breadth sweeps are smaller than in the midship bend. Under the stern bend he lists the sweep for the hollow and the sweep for the hollow mould. So this indicates the idea of diminishing radii numerically (Deane only shows that only graphically) and also shows that some parts of bends are not used along the complete length of a hull.
A second, more early, source is a so called RINA or Scott manuscript, which unfortunately has been sold several years ago and is not available to read. Before that Michel Daeffler had been able to use for his book "Formes de carène et navires de combat : L'invention du vaisseau de ligne en Angleterre (1560-1642)". I wonder does anybody here have an access to a copy of this MS?
Thank you very much!! I appreciate your thoughts.
For anyone in the U.S. whose interested, Keltridge's book hasn't been published, but there is a copy at Brown University. There is also at least one copy in Europe, but I can't remember how many, or where they are.
As it turns out, I actually have a copy of the Scott MS but, to obtain it, I had to agree not to quote it. That's no great loss. My quotes probably wouldn't be worth anything. The document is written in secretary hand, which is difficult to read. To make matters even more difficult, its author uses a lot of idiosyncratic characters. It would take me months accurately translate it, so that's a task best left in the hands of someone more competent than me.
It sure would be nice if someone would put information on ship design from the late 16th century (starting with Baker) through the 17th century all in one place, and compare the relevant works. As you no doubt know, the relevant information is scattered, a lot of it is unpublished, and some of it is difficult to find. I'm sure you'd be better equipped to do it than me. If you decide to start a thread, or even publish a book on this topic, I'd sure read it!
CHARLIE WHY NOT CHECK WITH WALDEMAR HE POSTS QUITE A BIT DONE MUCH GREAT REASEARCH BE KIND TO US ILLITERATES WHO WANT TO LEARN, HIT ME BACK. GOD BLESS STAY SAFE YOU AND YOURS DON