Dear Friends
I have received Hans's input on my calculations and seeing that he did not see the need to have me certified

, here I go with my idea:
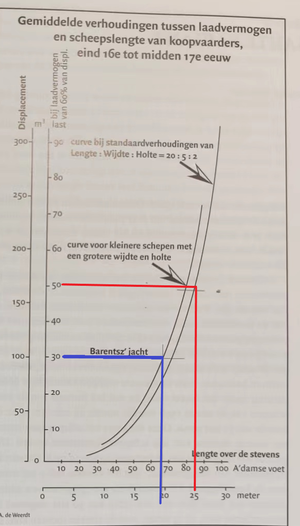
Below you will find a “certer” or building guideline for Dutch ships from the late 16th Century (such as the WB) up to the middle of the 17th Century. The Y-Axis represents the displacement in lasten while the X-Axis represents the length (from stem to stern) in meters.
View attachment 391545
The Blue guidelines are representative of a ship of 30 lasten as per Hoving and De Weerdt while the red lines indicate a ship of 50 lasten as per my theory.
Following the above certer we see that
a ship with 30 lasten will have an estimated hull length of approximately 19 meters. This equates perfectly to Hoving’s plans which indicate a hull length of 19,13 meters. De Weerdt has his hull length at 18.6m which is slightly shorter. The Kolderstok kit has a stem to stern length of 17.5 meters. In total, there is only a variance of 1.5m in length so it would be fair to say that all three are in the ballpark of the guidelines.
If we now focus our attention on
a ship of 50 lasten we will see that it equates to a stern length of
23 meters (measured on the inner curvature of the hull) and
25 meters when measured on the outer curvature of the hull.
Looking at Hoving’s drawings, we see that the ship (at the widest point) has a width of 6.088m which gives us a length/width ratio of 3.14. (19.13 meters hull length divided by 6.08 meters in width =
3.14).
De Weerdt’s plans show a ratio of 3.7 (18.6 meters in length divided by 4.95 meters in width =
3.7).
The Kolderstok kit has a ratio of 3.18 (17.5 meters in length divided by 5.50 meters in width =
3.18)
Proportionally, the Hoving drawings thus show the widest ship, followed by the Kolderstok model while De Weerdt's interpretation is the narrowest.
The million-dollar question is which ratio to follow? Despite my differences with Hoving, I tend to favor his ratio seeing that it was developed by the late Theo van Harpen - a hydrodynamic specialist. Thus, we know for a fact that Hoving's ratio is a plausible one in real life and would have resulted in a very good sailing ship - which the WB was by all accounts. The Kolderstok kit is very close to that of Hoving so it's very much a case of six of the one and half a dozen of the other.
'
According to Hans the
calculated width of the widest frame according to Zhdan's drawings is 7.8 meters (1:1). If I now apply Hoving’s ratio of
3.14 multiplied by
7.8 we arrive at a hull length of
24.492 meters - exactly that of a 50-lasten ship.
If I apply the Kolderstok ratio of 3.18, the hull would have a length of 24.8 meters - also perfect!
This would suggest to me
that the frames that the Russians found at Nova Zemlaya and on which the Zdhan's drawings were reportedly based
were those from a 50 lasten ship and NOT a 30 lasten one!
Whilst the frame widths of Zdhan are thus perfectly plausible, the hull/keel length will have to be increased to a 1:1 length of either 24.5m or 24,8 meters (1:1) while in 1:50 scale, it would result in a hull length of 490 cm (Hoving) or 496cm (Kolderstok).