Luckily we have Charlie 's work on this, looking at his work untill know I am convinced he will discuss it all in his coming posts, we will look forward to it.Hi Kurt;
That would mean re-reading Sephton's book, which is rather an ordeal. I have already read it twice, and that is as much as I can bear. His style of writing does not flow smoothly, and most of the illustrations are of poor quality. I look upon Sephton's book as a source of some information about her, but not as a source for serious research, due to his lack of references. His book is more a guide to what information might exist somewhere, waiting to be located again, which Sephton presumably saw but does not give a reference to help locate.
-

Win a Free Custom Engraved Brass Coin!!!
As a way to introduce our brass coins to the community, we will raffle off a free coin during the month of August. Follow link ABOVE for instructions for entering.
-

PRE-ORDER SHIPS IN SCALE TODAY!
The beloved Ships in Scale Magazine is back and charting a new course for 2026!
Discover new skills, new techniques, and new inspirations in every issue.
NOTE THAT OUR FIRST ISSUE WILL BE JAN/FEB 2026
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
17th Century Ship Design and the Sovereign of the Seas (1637)
Hopefully CharleyT will address features of the vessel which are not documented, with statements to that effect. Often we waste huge amounts of time looking for information on a specific feature which does not exist, and it's helpful to know that up front. I can't tell you how many hours I've spent looking for evidence of that booby hatch and companion way McKay placed on the halfdeck, a useless duplication of the ladder located just forward of that on the same deck. It turns out to have zero basis in every source I can find.Luckily we have Charlie 's work on this, looking at his work untill know I am convinced he will discuss it all in his coming posts, we will look forward to it.

- Joined
- Mar 22, 2024
- Messages
- 396
- Points
- 168

Further to Charlie's answer above, and your question, volume V is available second hand very rarely. You could pay for access to Taylor and Francis, but it will not tell you anything which has not already been said, as the information given in Anderson's note is limited. The dimensions are available in the NRS volume for 1918, the autobiography of Phineas Pett, which is easier to find secondhand. All that is missing in this latter volume are the radii of the three sweeps which Charlie has used, and which are given in the Sergison Papers (Anderson did not specify which of the many volumes it was in)
There is a free download of Phineas Pett's autobiography on Project Gutenberg. https://www.gutenberg.org/ebooks/51357 There is an actual scan of the original- with images - also available free on https://archive.org/details/autobiographyofp00pettuoft/page/n5/mode/2up
- Joined
- Mar 22, 2024
- Messages
- 396
- Points
- 168

Also a Scan of the book at https://archive.org/details/autobiographyofp00pettuoft/page/124/mode/2up?view=theaterThere is a free download of Phineas Pett's autobiography on Project Gutenberg. https://www.gutenberg.org/ebooks/51357
A fascinating read. Sorry - duplicate post.
To put it in a nutshell, stay away from the tables in the appendices. For example, Appendix 8 lists Pennington's (not Pett's) molded breadth, and provides a measurement of the gun deck's length even though the Sovereign's deck length was not measured at its launch (the figure Sephton gives is from later). Sephton has also relied on secondary sources instead of primary resources. So, a lot of Appendix 8 appears to be from Charnock's 1801 book. The same is true of appendices 20 and 21. These are based on previous plans for the Sovereign that are likely incorrect. Then, too, much of the information Sephton gives is extraneous, and can easily be misleading.
Thanks you CharlieT. That was extremely helpful.To put it in a nutshell, stay away from the tables in the appendices. For example, Appendix 8 lists Pennington's (not Pett's) molded breadth, and provides a measurement of the gun deck's length even though the Sovereign's deck length was not measured at its launch (the figure Sephton gives is from later). Sephton has also relied on secondary sources instead of primary resources. So, a lot of Appendix 8 appears to be from Charnock's 1801 book. The same is true of appendices 20 and 21. These are based on previous plans for the Sovereign that are likely incorrect. Then, too, much of the information Sephton gives is extraneous, and can easily be misleading.
Section IV: The Sheer Plan
The discussion now turns to the sheer plan. The sheer plan shows a ship as viewed from its side. This section begins the same way a model is started, by focusing on the keel, stem, and sternpost.
The Keel
Pett tells us that the Sovereign’s keel was 127 feet long. It was measured using the “touch” method. This was the only method of measuring the keel that was of interest to master shipwrights. (Endsor 2020, 62) With this method, the keel’s length is measured from a perpendicular dropped from the sternpost’s aft end to a perpendicular dropped from the spot where the rabbet starts to curve upwards at the bow. (Endsor 2020, 62). This latter point is called “the “touch.”The Newton Manuscript would have us make the keel’s 2 to 3 times as long as the breadth. For the Sovereign, this means a keel that is somewhere between of 92 feet 4 inches and 138 feet 5 inches long. The Treatise tells us that the length of the keel should be 25/9 of the breadth, so it would have the Sovereign’s keel be approximately 128 feet, ¼ inches long. Deane would make the keel 10/3 the breadth, or a little over 153 feet 10 inches. The substantial difference between the two earlier sources and Deane reflects the change in keel:breadth ratios previously mentioned.
As previously discussed, the Sovereign’s keel was 19 ¼ inches square amidships. Attached to its underside was a false keel. Its purpose was to protect the keel. It was approximately 5 inches thick, making the entire assembly 24 ¼ inches high in cross section.
Keels tapered both fore and aft of the midship bend. Although the keel’s taper is difficult to see on models, and particularly those of smaller scale, it is nevertheless useful to taper it anyway. Doing so helps show the full extent of the expansion of the stem and sternpost at their heads, which will be discussed in the next two sections.
The Treatise, Bushnell, and Deane are silent on how the keel tapers. The Newton Manuscript tells us “the breadth of the keel at ye after part of the sternpost must not be more than ¾ nor less than ⅔ parts of the keel [at the midship bend],” meaning that the aft end of the Sovereign’s keel should taper to a width between 12 5/6 inches and 14 7/16 inches. Keltridge’s 1675 manuscript suggests that the keel tapered aft from an amidships width of 18 ½ inches to 12 ½ inches, which is a reduction to 67.57% of the its maximum width. Reducing the Sovereign’s keel by this percentage makes its keel taper to 13 inches, which is like the Newton Manuscript’s minimum aft keel width. I have used the latter width rounded to the nearest ¼ inch. This makes the keel 12 ¾ inches wide at its aft end.
The Newton Manuscript also tells us that “the breadth of ye keel at the forepart at the touch of the stem must not be more than 11/12 nor less than 3/4” of keel’s width at the midship bend, yielding a width for the fore end of the Sovereign’s keel that is between 14 7/16 inches and a little over 17 5/8 inches inch. I have used the Newton Manuscript’s minimum width because it was written around the time of the Sovereign’s design. When rounded to the nearest ¼ inch, it produces a keel whose fore end is 14 ½ inches wide. It would also be reasonable to use Keltridge’s taper. The fore end of his keel is 17 inches wide on his ship, which translates to about 17 5/8 inches on the Sovereign.
Where the tapers started is unknown. No contemporary English source mentions it. The earliest English source that does seems to be a treatise by Samuel Thearle, published in 1876. (Thearle 1876) He tells us that we are “to commence the taper at a distance of one foot from the stem or stern post for every quarter of an inch difference between the siding of the lower part of the stem or stern post and that of the keel at the midships.” (Thearle 1876, 174) Expressing this as distances from the Sovereign’s midship bend produces relatively short tapers; the fore taper begins 23 feet fore of the midship bend, and the aft taper begins 58 feet 8 inches aft of it.
A better approximation of the keel’s taper might be had from the taper of the Vasa’s keel. This is a ship from another nation (Sweden), but it is a contemporary of the Sovereign. Nineteenth century ships like those discussed by Thearle were shaped differently than those of the 17th century, and shipwrights from the former time had a better understanding of hydrodynamics than those in the 17th century, so the way they designed their keels may have differed. The Vasa’s keel appears to have been designed so the forward 20% of its keel would taper, the middle 30% would be straight, and the aftmost 50% of the keel would also taper. (Hocker) Using these proportions for the Sovereign’s keel produces a fore taper that starts 16.93 feet fore of the midship bend, and an aft taper that starts 21.17 feet aft of this bend. These tapers are used in the present reconstruction.
The keel was too long to be made from a single timber. Typically, it was made of several pieces joined together by scarf joints. Four pieces seem reasonable for the Sovereign.
References
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.Hocker, Fred. Personal Communication.
Thearle, Samuel J.P. 1876. Naval Architecture. London and Glasgow: William Colliins Sonse, & Company.
Section IV: The Sheer Plan (continued)
The Sternpost
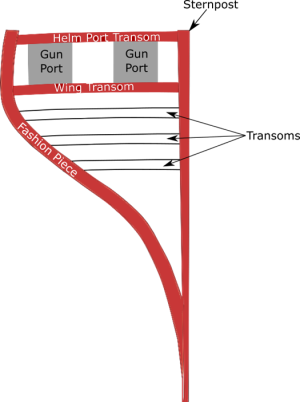
The sternpost is a massive piece of wood to which the rudder is attached. It is a major structural component of a ship. It is not visible on the Pett painting, the Payne engraving, or the van de Velde drawing.The post is part of an assembly whose complexity is largely ignored by the Treatise, the Newton Manuscript, Deane, and Bushnell. The horizontal timbers that were attached to it are of particular relevance to the present discussion. These timbers are known as transoms (Figure 15). Their curves give the stern its outwards curve. The Sovereign’s transoms also arc upwards in a manner that roughly parallels the cambers of the gun decks. (Fox) The transoms’ fore ends are attached to a complexly-curved timber called the fashion piece.
Figure 15. Rear View of the Transoms
Note: The figure is a representation of a generic stern. It is not intended to represent the Sovereign’s stern. The figure is not drawn to scale.
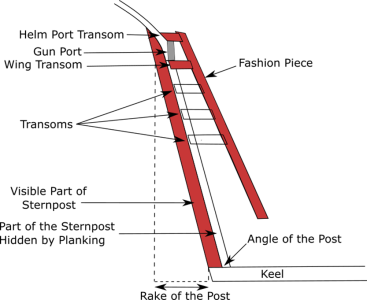
The attachments of the transoms to the post and fashion piece can also be seen from the ship’s side (Figure 16) These attachments are not visible from the outside. They are hidden by planking. The entire sternpost is also not visible from the outside. Part of it is also hidden by planking.
Figure 16. Side View of the Transoms
Note: The figure is a representation of a generic stern. It is not intended to represent the Sovereign’s stern. The figure is not drawn to scale.
The wing transom is the most important transom for the present discussion. The post’s height was measured as the height of this transom’s top above the keel’s bottom. Deane tells us that the keel’s bottom is “with the false keel so well as the main keel.” The post’s height was measured this way even when the post extended above this transom, which was the case on the Sovereign. The post is barely discernable on most drawings of the Sovereign’s stern, but a drawing by van de Velde from the mid to late 1600’s (Figure 17) shows it extending a little above lower gun deck’s chase ports. Neither the Treatise nor Deane say they run their posts above the wing transom. However, Bushnell, who also draws his post to the wing transom, notes that “if the Stern post were continued to the height of the Tiller and another Transome fay’d there for the Tiller, to run on, it would steady the quarters of the Vessel very much, and do good service.”
Figure 17. Van de Velde’s 1685(?) Portrayal of the Sovereign’s Stern
National Maritime Museum.
Note: The is a portion of drawing by van de Velde. The National Maritime Museum tentatively lists it as dating from around 1661 (National Maritime Museum) but a later date, possibly 1685, is more likely. By the time it was drawn, the Sovereign’s appearance had changed from when it was launched. One of the changes included widening its wing transom. The sternpost can be seen just behind the rudder.
The wing transom forms the sills of the lower gun deck’s stern chase ports. The helm port transom forms the ports’ tops. The wing transom is the widest of all the transoms. Its depth (top to bottom) on the current plans is the same as the width of the upper main wale, 16 inches. I have set the depth of the helm port transom at 14 inches. This smaller size helps create room for the tiller to pass between it and the middle gun deck’s beams.
Pett gives us very little information about the Sovereign’s sternpost. He only tells us that its rake was 8 feet, meaning that the post’s aft face at the top of the wing transom was 8 feet aft of the aft end of the keel. Since he does not tell us the post’s height, we can draw an infinite number of lines to represent it. Fortunately, the situation is not this dire.
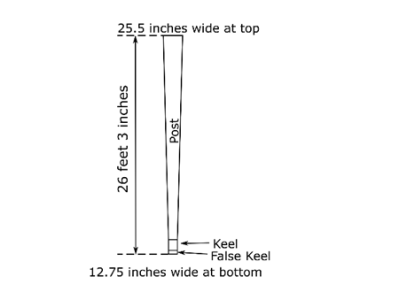
A document from about 1640 gives us information we can use to determine the post’s height. It tells us, in part, that the ordinance was five feet from the water in the midships, and 6 ½ feet from it abaft. (52) Assuming that the guns were centered in the ports, we can now deduce that the ports abaft were 18 inches further from the water than those amidships, though the meaning of “abaft” is ambiguous. It could refer to either the heights of the aftmost ports on the ship’s sides or the heights of the stern chase ports. I have taken it to mean the latter because the height of these ports was of greater importance to shipwrights. If we now recall that Phineas Pett tells us that the ports at the midship bend were five feet from water, the chase ports must be 6 ½ feet from it.[1] Since the draft at the stern is 19 feet 9 inches (the draft will be discussed in a later section), we wind up with a post that is 26 feet 3 inches high (the post is 26 feet 7 inches high if we take “abaft” to refer to the ports along the ship’s sides).
This post’s angle is 18.27° (it is 18.04° if the higher post is preferred). Both the Treatise and the older Newton Manuscript tell us that this angle is appropriate. The former tells us that the angle of the post should “never recline from the zenith [of] more than an angle of 22 [degrees] no[r] less than 18 [degrees].” The latter says that “the rake of the sternpost aftward must take his proportion from the depth & shall be any angle of degrees, & must not be more than 22 ½ degrees nor less than 18.”
Proportional rules from later 17th century authors give the Sovereign a post that is more vertical than the Treatise or the Newton Manuscript suggest. Keltridge’s post has a height that is 23/24 of the transom’s width. His rake is ¼ of the post’s height so, when applied to the Sovereign, which had a 28-foot wide transom, we find a post with a height of 26 feet 10 inches, a rake of 6 feet 8 ½ inches, and an angle of 15.13°. Battine gives similar proportions. He tells us the post’s “length by the rake from ye bottom of the keele” should be 22/24 of the transom’s width, and that its rake should be ¼ to ⅕ its length. This gives rise to a post that is 25 feet 8 inches high, that has a rake that ranges from about 5 feet 1 ¼ inches to 6 feet 5 inches, and whose angle ranges from 12.35° to 15.31°.
Deane’s proportional rules are also worth examining because others have used them to reconstruct the Sovereign. Deane would have us compute the post’s length as ⅔ the breadth minus one half foot. It is unclear whether the “length” he refers to is the length along the post’s aft face, or the length of a perpendicular that runs from the keel’s bottom up to the wing transom. Assuming the former puts his proportions in the most favorable light and, when this is done, his sternpost is 30.28 feet long. We can insert then this information into the Pythagorean Theorem to find the post’s height, which is 29.32 feet (The height is 30.28 feet if we assume Deane is referring to the height of the perpendicular). The rake of Deane’s post is ¼ of its length, or 7.57 feet, which is shorter than Pett’s rake of 8 feet. This post’s angle is only 15.50° (the angle is 15.00° if we assume Deane is referring to the height of the perpendicular).
We can somewhat reduce the height of Deane’s post’s, and thereby increase its angle by using Pett’s rake, but the angle is still only 16.40°. This relatively small angle occurs because the amount the post can recline backwards is limited by Pett’s 8-foot post rake so, when the post is relatively high, it becomes more vertical (Figure 18). This makes its angle is smaller (Figure 19). These considerations lead us to conclude that it is unlikely that Deane’s proportions were used to design the Sovereign’s post.
Figure 18. Changes in Post Height and angle when its Rake is Constant
Note: The figure shows a lower post (in pink) and a higher one (in grey). Both are drawn to their respective wing transoms. The lower post does not need to be very long to reach a rake of 8 feet, so it has a relatively large angle. The higher post needs to be longer to reach the rake, and this makes its angle smaller.
Figure 19. Effect of Post Height on its Angle
The Treatise’s author allows for a range of post heights. This is implied by the varying post lengths he allows. These range from a post whose length is “never more than ⅔ the breadth” to a post whose length is never “less than ½ the depth from the skeg to the counter.” However, the author implies an optimal proportion for the post’s height when he provides a proportional rule that describes the ship’s depth at the wing transom.[2] He says it should be 100/75 of the depth. This yields depth of about 25 feet 7 ¾ inches high on the Sovereign. When we add in the keel’s height, we obtain a post that is almost 27 feet 8 inches high. This is too high. It yields an angle of only about 17.33°. This is one of several differences between the Treatise and the Sovereign that we will find at the stern .
We can now turn to the post’s other dimensions. When viewed from the side, sternposts of the Sovereign’s era were wider at their bases than at their tops. Neither the Treatise nor the Newton Manuscript tell us how much. Deane only tells us that its width should be “so big as your piece will afford.” Keltridge gives us a clearer picture. He tells us that the dimensions for the entire post are: “Fore and afte at ye head – 1’ 9” and “Fore and afte alow – 2’ 7”. Only part of the post was visible because the rabbet into which the planking was inserted was carved into it. Keltridge tells us that the exposed part should be 8 inches wide at the wing transom, and 1.5 feet wide at the base. I have used Keltridge’s dimensions without adjusting them for the differences between the width of his keel and that of the Sovereign.
The sternpost is, when viewed from astern, wider at its top than at its bottom. Making the post narrower at the bottom provided a cleaner flow of water to the rudder, while making it wide near its top provided more support for the transoms. Accordingly, the sternpost on the present plans is 12 ¾ inches wide at its bottom. This is the width of the aft end of the keel. Keltridge makes “the breadth of ye sternpost at ye head” twice the width of his keel’s aft end. I have followed suit, so the top of the post is 25 ½ inches wide. Figure 20 illustrates the post’s taper.
Figure 20. The Post as Viewed from the Stern
References
Fox, Frank. "Personal Communication."National Maritime Museum. 1661? Portrait of the 'Royal Sovereign'. Accessed July 14, 2021. https://www.rmg.co.uk/collections/objects/rmgc-object-157854.
Porter, Mark. "Personal Communication."
[1] The ports that are truly at the ships middle are also about five feet from water, so we obtain the same result no matter how we define “amidships.”
[2] The depth is the height of the breadth at the stern as measured from the keel's top. In the present case, the depth is the post's height as measured from the keel's top.
Last edited:
OH WOW,WOW. GOD BLESS STAY SAFE ALL DON
Section IV: The Sheer Plan (continued)
The Stem
The stem constitutes the most forward part of the bow. It can be thought of as a curved extension of the keel. The Treatise tells us that “the stem is one or more pieces of large compass timber scarfed and bolted together, swept out by a circle …. It is fastened to the fore top of the keel with a strong scarf and hath two large rabbets on each side thereof, to receive the butt ends of the planks forward…”. Notice that the rabbet was notched into the stem.We need to consider two characteristics of the stem before we can draw it on our plans. The first of them is its rake, which is a measurement of how far the stem’s fore face protrudes from the keel’s fore end at a specified height above the keel. The second is its radius because, in the Sovereign’s time, the stem was drawn as part of a circle.
The relationship between the stem’s radius and rake varied. Early in the 17th century, the stem’s radius was greater than its rake, so it never became vertical. Deane, however, describes a radius that equals the rake, so his stem is vertical at its upper end. In both cases, the stem was drawn tangentially to the keel. (Lavery 1984, 7-9)
This tangential relationship ultimately changed, causing the stem to abruptly rise. This is seen in Keltridge’s 1684 drafts. The radius of his non-tangential stem is so large that it barely curves and, therefore, the stem runs along a more vertical course than in earlier ships. Some shipwrights even used a small, short radius near the keel and combined it with a vertical straight line. (Lavery 1984, 7-9)
The driving force behind making the stem vertical was a desire to increase the keel’s length so that it would occupy a greater proportion of the ship’s length. (Lavery 1984, 7-9) The advantages of a vertical stem were that it increased buoyancy at the bow, reduced pitching, and helped keep the keel’s middle from bending upwards (hogging), which could cause the hull to snap or crack. (Endsor 2020, 63) Vertical stems became common as the result of an Admiralty Board discussion in 1677. The gun deck’s length became a standard measurement from this time on. (Lavery 1984, 9)
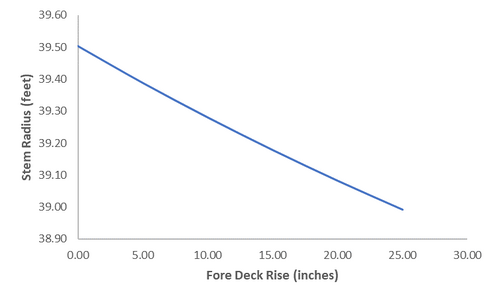
The Sovereign’s stem follows the older style and not Deane’s, so its radius was larger than its rake, and it did not become vertical. Its rake was measured as the horizontal distance from the touch to its fore face at the level of the middle gun deck. (Fox) Pett tells us this was 38 feet. Since the stem’s rake was measured along the middle gun deck, its radius depends on that deck’s height. It becomes smaller as the deck’s height increases (Figure 21).
Figure 21 Deck Height and the Stem’s Radius
Note: Deck heights are expressed as how much the deck rises from the midship bend to the bow. For example, a 20 inch deck rise means the deck’s fore end is 20 inches higher than it is at the midship bend. Deck rises are used because we already determined the middle gun deck’s height at this bend (it is 27.31 feet). This was discussed in the section devoted to the midship bend.
Pett only gives us the stem’s rake, so we must find its radius on our own. The Treatise, Deane, the Newton Manuscript, and Bushnell do not tell us how to do this, but it is reasonable to assume that Phineas Pett knew how to find it before putting the stem on the Sovereign. It would have been too difficult to shape otherwise.[1] Euclid’s intersecting chords theorem, which Pett would have learned while attending Cambridge, provides a reasonable method. Applying this theorem in conjunction with the height of the middle gun deck used on the current plans (this has been discussed in the section on the midship bend, and will be mentioned again later) gives a radius for the Sovereign’s stem of about 39 feet 6 inches.[2]
The radius of the Sovereign’ stem is greater than the radius Treatise would have us use. It tells us that the “best proportion” for the radius is 7.125 feet for every 9 feet of breadth. For the Sovereign, this works out to be just a little more than 36 feet 5 ½ inches. The Sovereign’s radius is even further from Deane’s recommendation. He tells us it should be should be ¾ the breadth, [3] which is 34.63 feet for the Sovereign.
Since Deane’s stem radius is also his rake, the Sovereign’s rake is also bigger than Deane’s. We might expect this because the Sovereign is a bigger ship. However, the Sovereign’s rake was proportionally smaller than in earlier ships. Bushnell tells us that these ships had a rake that “…was the whole breadth of the Ship.” Bushnell goes on to explain that “too much rack with the Stem doth a great deal of damage to any Ship.” The problem was that there would be “want of Body, to lift it, so that it must of necessity be detriment to the Vessel when she saileth against a head sea, and a great strain to her.”
Mainwaring expands on this by telling us:
“A great rake forward on gives a ship good way and makes her keep a good wind, but if she have not a good full bow it will make her pitch mightily into the head sea; besides, it doth mightily charge the ship because it doth overhang the nail. And if a ship have but a small rake she will commonly be too bluff, and so meet the sea too suddenly upon her bows, which will hinder her going through much. The longer a ship’s rake is, the fuller must be her bow. The best conditioned ships have neither too much nor too little.” (Mainwaring 1922, p 206-207)
The Pett painting suggests that the Sovereign’s stem is like Deane’s in that its width, when viewed from the side, is constant from its bottom to its head. We can replicate this by making the radius of the stem’s inner face equal to that of its outer face minus the keel’s depth (not including the false keel). The Treatise’s stem becomes wider at the top.
When viewed from the front of the ship, the bottom of the stem was narrower than its top. The base of the stem on my plans equals the width of the keel’s fore end, or 14 ½ inches. My plans make the top of its stem the same thickness as the top of the stern post, 29 inches. It would also be reasonable to use Keltridge’s dimensions. The stem is 30 inches wide on the first rate ship he describes and, after correcting for the difference between the width of his stem’s base and that on the current plans, it would be about 26 ¼ inches wide on the Sovereign.
The stem, like the keel, was too big to make from one piece. It was composed of two pieces on smaller ships, but three are more appropriate for a ship as large as the Sovereign. These pieces were joined by scarf joints.
The stem is problematic on some kit-built models of the Sovereign. These kits do not carry it far enough upwards, and end it below the beakhead’s deck. The stem should run up far enough to make the decoration on top of it higher than the beakhead’s walls (the stem on the current plans is drawn from the bottom of the keel (not the false keel) up to a height equal to the rake, 38 feet). This decoration is Cupid riding a lion. Heywood (1637) describes the stem as the location of this decoration when he says “I began at the Beak-head, where I desire you to take notice, that upon the stemme-head there is Cupid, or a Child resembling him, bestriding, and bridling a Lyon [underlining added].” Phineas Pett clearly planned to have a decoration here, as shown by his son’s painting. Payne also clearly shows this decoration on top of the stem. Van de Velde also shows it on the stem-head, which he has colored solid dark grey. Since the decoration is difficult to see in his drawing, I have shown it circled in red in Figure 22. Kits that do not run the stem high enough erroneously put this decoration on a box-like structure that sits on the beakhead’s deck or on the bowsprit.
Figure 22. The Decoration on the Stem Head as Depicted by van de Velde
[1] Innumerate shipwrights could have used a template worked out from experience. This is only practical on ships of similar sizes. It is not practical on the Sovereign because no existing ships were enough like it.
[2] This figure was generated by the mathematical model that underlies this reconstruction. I have rounded all such figures to the nearest ¼ inch.
[3] Deane actually describes the rake, but the radius and the rake are equal on his ship.
References
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.Fox, Frank. "Personal Communication."
Lavery, Brian. 1984. The Ship of the Line. Vols. Volume II: Design, Construction and FIttings. Londin: Conway Maritime Press.
Mainwaring, Henry. 1922. The Life and Works of Sir Henry Manwaring. Edited by G.E Manwaring and W.G. Perrin. Vol. 2. 2 vols. London: THe Navy Records Society.
Last edited:
Totally agree with you. Too many models have a stem and stern post as well as the knee of the head that are the same thickness from the top down to the keel which was never the case.Keels tapered both fore and aft of the midship bend. Although the keel’s taper is difficult to see on models, and particularly those of smaller scale, it is nevertheless useful to taper it anyway. Doing so helps show the full extent of the expansion of the stem and sternpost at their heads, which will be discussed in the next two sections.
Allan
Last edited:
Section IV: The Sheer Plan (continued)
The Swimming Line
The swimming line is a line that follows the ship’s draft from stem to stern. It was measured as the vertical distance between the water and the keel’s bottom. It is the depth at which a loaded ship “swam.” (Abell 1948, 47) In the present case, “loaded” refers to a partially loaded ship, not a fully loaded one. (Ferriero 2007, p 196) The definition of “partially loaded” varied. Accordingly, Pett lists the heights of the ports above the swimming line “with four months victuals” and “with sixth months victuals.” Methods for precisely determining how high the swimming line was did not exist in the early 17th century, so the term “estimated swimming line” is probably a better description of what these shipwrights used.Properly drawing the swimming line is critical to reconstructing the Sovereign. This line was also of critical importance to shipwrights. The Treatise describes it as “a principal thing to be regarded for the good qualities of a ship. From that line are set off the decks and ports for the ordnance, higher or lower as we will have them lie to pass.” Phineas Pett apparently followed this practice. He thus expresses the height of the Sovereign’s ports in terms of their height above the swimming line.
The Treatise’s author is not unique in understanding the importance of the swimming line. Bushnell tells us that “the draught of the water ought to be respected first, and then the lying of the Ports for the convenience of Ordnance,” so he tells us to “… draw the water line …. Higher abaft than afore, for the most Ships sail by the Stern….”
Deane is even more emphatic. He says that “the water line … is of so great concernment that the whole good or bad quality of a ship depends on that design and is, or ought to be, the principal line regarded in the whole art of the master shipwright.” He goes on to complain that not all shipwright’s were adept at determining how high it should be, telling us that:
“to lay down this line as it ought to be is of great worth and advantage on every man-of-war, which, if it had been thoroughly understood, we had never had such great mistakes in the navy as we have found, to the confounding of vast treasure in the kingdom, by sometimes lengthening them or by girdling them of great thicknesses, or at other times making them fuller or leaner bowed and perchance furring out [1] or thickening the run or the way….”
The Newton manuscript and the Treatise offer only a rudimentary treatment of the swimming line. The former merely tells us “The depth must be in proportion to the breadth & must not be more then [sic] ½ thereof nor less then [sic] ⅓ unless there be such a necessity to have such to draw little water to do some service in a river or such like where the water is but shallow.” This was widely known, and it explains why the English, who had access to deep water harbors, built ships that were relatively narrow, while the Dutch, whose harbors were relatively shallow, built relatively broad ships. The narrow ships draw more water, and the broad ships draw less.
The Treatise only tells us that a ship’s draft at the midship bend lies at the intersection of the futtock sweep and the “upper sweep.” Its description of how to draw the rest of the line is unclear but, if followed literally, it leads to a swimming line that is parallel to the keel.[2] Shipwrights knew better than this. The Treatise’s author knew better because, when discussing deadrise, he tells us that shipwrights “will have the ship draw more water abaft than afore.” The above-mentioned quote from Bushnell echoes this, and Mainwaring agrees by saying; “…for you must know a ship never draws so much ahead as she doth astern, for if she should she would never steer well.” (Mainwaring 1922, 254) Indeed, this was even known by William Bourne, whose 1578 book tells us “all ships do draw more water at the stern, than they do at the head.”
Neither the Newton manuscript or the Treatise touch upon Archimedes principle, which tells us that if something is heavier than water, it will sink, and if it is lighter than water, it will float. Yet, shipwrights knew this well before these two documents were written. Thus, the 1578 writings of William Bourne (Bourne 1578) tell us;
“Looke what quantitie of the Ship is buryed in the water, that is to say, from the edge of the water downwards: then if there were a vessell or great thing made of the proportion of the moulde of a Shyppe, as much as is buried in the water, if that were filled with that water that the ship were in, the water shoulde be of iust equall waight, that the Ship were of, with all her tackle and implements in her.”
Bourne also goes on to recognize that water from different sources has different weights, with the implication that the amount of water a ship displaces depends on the kind of water it is in. Bourne thus tells us “And now suppose that the water was of our water, here at Gravesend, and that is not of the lightest sort, neither of the heaviest sort….” He then goes on to provide three methods for determining a ship’s displacement though, they would only work for a ship that was already built, and would not be useful when designing a ship. (Olaberria 2018, pg 67) Bourne does not give the impression of describing something new or obscure. Using Archimedes' principle to describe why ships float was likely well known at the time of his writing. (Olaberria 2018, pg 68)
Bushnell’s and Deane’s works are clearly based on this principle. The used it to estimate the amount of ballast and other loads that would bring the ship to its correct waterline. (Ferriero 2007, 199) In Bushnell’s words:
“the weight of the same body of the same water that the ship swimmeth in, shall be the exact weight of the ship, and all things therein, loading, rigging, victuals included therein: then if the ship be measured to her light mark as she will swim at being lanched, the weight of so much water being taken or substracted from the weight of the water when she is laden, the residue shall be the weight that must load her, or her ability of carrying, called her burthen: by this means you may know the weight of the ship light, and what she will carry to every foot of water assigned to her, which can be done by no general rules in Arithmetick, because of their great irregularity, according to the differing minds of Ship-wrights…”
Despite his pessimism about the value of “Arithmetick,” Bushnell goes on to outline his method, though his description is incomplete “because it will much increase my Treatise, and augment the Price, which might prove more prejudicial to young men, than advantageous.”
Deane’s summarizes his approach by saying “the principal is to measure the ship’s body underwater and find how many feet it contains, and her weight of body is so many 64 lbs as there shall be square feet in that body under water and no more.” The figure “64 pounds” refers to the weight of water, and he tells us “Standard salt water is just 64 ¼ of an ounce to 12 inches square, every way of measure.” On the other hand, “in the River Thames a foot square weigheth 63 lbs 12 oz, spring water 62 lbs 11 ⅛, rain water 62 1 ½.” These weights were probably not original to Deane. Bushnell also takes credit for measuring them when he says “I have proved by the Thames water, that fresh Water is lighter than salt water; so then salt water being heavier than fresh, causeth that a ship swimmeth deeper in the fresh water than in salt,” but he may be taking too much credit. As mentioned above, William Bourne was aware of at least some of this.
Deane is often credited with discovering how to determine a ship’s draft. Indeed, Samuel Pepys does this. (Ferriero 2007, 197) However, Phineas Pett did this for the Sovereign long before Deane’s work and, at about the same time, Phineas’ son and nephew (both named Peter) were also able to estimate the drafts of their ships, and how far above water their ports would be above it. (Ferriero 2007, 196) This was over three decades years before Deane wrote his Doctrine. Importantly, and despite the self-promotional air of Deane’s Doctrine, Deane never takes credit for discovering how to determine the draft. Lavery (Lavery, Deane's System 1670, pg 25) has even suggested that Deane implies the method was available to any shipwright who would “take the pains, or his skill afford so much of that art.”
We cannot know exactly how Phineas Pett determined the height of the Sovereign’s swimming line, but the preceding discussion of William Bourne’s work suggests that Pett was using basic principles that had been known among shipwrights for some time. He was clearly considering the ship’s weight and, therefore, Archimedes principle because he reports that the ports at the midship bend are further from water when the Sovereign carried “four months victuals” than when it carried “six months victuals.
Knowing only the distances of the ports from water at the midship bend is not enough to allow us to draw a swimming line. We also need to know where it ended at the bow and stern. Pett does not tell us this, and the Treatise and the Newton Manuscript are once again silent on this topic. Bushnell’s drawings suggest that he drew his line from the stem’s inner face to the post’s inner face. Deane’s drawings are inconsistent. In one place he draws his line like Bushnell, but he more commonly drew it from the aft side of the post to the fore side of the stem. I have used Deane’s latter method, though there is little practical difference between this method and Bushnell’s.
With this information in hand, we can turn to what Pett tells us about the Sovereign’s swimming line. He only says that it was 18 feet 9 inches from the keel’s bottom at the midship bend, so we need to find its height at the bow and stern. We begin by considering a “rule of thumb” for 3-decked ships of this era; they drew 2 feet more water at the stern than at the bow (Fox). (Laughton 1932) Some have combined this this “rule” with the Sovereign’s draft at the midship bend to deduce that it drew 19 feet 9 inches of water at the stern, and 17 feet 9 inches at the bow (Laughton 1932) (here, we are using the figures for a ship provisioned with “four months victuals”).[3] However, this deduction requires modification. The reason for this can be seen when we plot these points along the Sovereign’s hull. When we do, we find that, unlike a proper swimming line, they do not form a straight line.[4] The result is that the straight line that best fits them does not run through any of them (see Figure 19). This means that we need to modify either the point at the bow, or the one at the stern.[5]
Figure 23. Drawing the Swimming Line Using a “Rule of Thumb”
Note: Red dots indicate heights of 17 feet 9 inches, 18 feet 9 inches, and 19 feet 9 inches at the bow, midship bend, and stern, respectively. The line is the line that best fits these points. It cannot be used because it does not run through any of them, including the point at the midship bend that Pett provides. The drawing is not to scale.
One way to modify these points is to assume a 19 foot 9 inch draft at the stern, and then solve for the draft at the bow. This is arbitrary, but it is also realistic. The weight of the Sovereign’s aft upper decks and its stern chase guns suggest that it is prudent to make the stern draft as deep as possible. Any other modification of the “rule of thumb” that maintains the midship bend draft that Pett gives us does not accomplish this. Accordingly, the current reconstruction estimates that the Sovereign’s designed draft was 19 feet 9 inches and the stern, and 17 feet 11 inches at the bow.[6] The difference between the drafts at the bow and stern, which is the ship’s trim, is 1 foot 10 inches. The trim is not meaningfully affected by how much weight a ship carries. We find a nearly identical trim when we examine the draft of a fully loaded ship.[7]
Modelers who wish to mount their ships to depict the Sovereign as it looked while sailing will want to take its trim into account, and mount their models with the bow higher than the stern, instead of placing their keels parallel to the surface on which the model rests.
[1] Girdling was the adding of timber to the outside of the underwater part of the hull. It was done to make ships float higher. Furring out is a more radical modification in which the underwater planking is removed, and additional timbers attached to the frames. Afterwards, the ship is re-planked. The run was apparently the part of the underwater part of the hull as it narrowed towards the stern, and the way was the narrowing of the ship at both ends. (Lavery, Deane's Doctrine of Naval Architecture, 1670 1981, 55)
[2] At least one author has literally followed these instructions while developing plans for another ship.
[3]Laughton (Laughton 1932) also provides estimates of the Sovereign’s draft, but he assumed Pennington’s design, which had a draft of 19 feet 6 inches amidships, was used. This is 9 inches more than the draft Pett gives. If we subtract 9 inches from Laughton’s drafts at the bow and stern (18 feet 6 inches, and 20 feet 6 inches, respectively), we obtain the drafts suggested by Frank Fox; 17 feet 9 inches at the bow, and 19 feet 9 inches at the stern.
[4] Linear regression was used to determine whether the 3 points fell along on a straight line.
[5] We cannot modify the point at the midship bend because it is given by Phineas Pett. We could, of course, decide to modify the points at both the bow and the stern. The decision that we need to modify only one of them is a simplifying assumption.
[6] I have rounded this figure to the nearest ¼ inch. The precise draft at the bow is 17.919967 feet, leading to a precise trim of 1.8303 feet.
[7] The precise trim is 1.8380 feet. Figures for a fully loaded ship were taken from Laughton. (Laughton 1932) They are 22 feet 6 inches at the stern, 21 feet 6 inches at the midship bend, and 20 feet 6 inches at the bow. These figures do not form a straight line, so the drafts at the stern and midship bends were retained, and the draft at the bow was solved for. Laughton’s draft at the midship bend is different from Pett’s draft of 21 feet 3 inches.
References
Abell, Sir Westcott. 1948. The Shipwright's Trade. Cambridge: Cambridge University Press.Bourne, William. 1578. A booke called the Treasure for traveliers, devided into five Bookes or partes, contaynyng very necessary matters, for all sortes of Travailers, either by Sea or by Lande, written by William Bourne. London: Imprinted for Thomas Woodcocke.
Ferriero, Larrie D. 2007. Ships and Science. Cambridge: Massachusetts Institute of Technology.
Fox, Frank. n.d. "Personal Communication."
Laughton, L. C. Carr. 1932. "The Royal Sovereign, 1685." The Mariner's Mirror 18 (2): 138-150.
Lavery, Brian. 1981. Deane's Doctrine of Naval Architecture, 1670. London: Conway Maritime Press.
Lavery, Brian. 1670. "Deane's System." In Deane's Doctrine of Naval Architecture, 1670, by Anthony Deane, 128. Annapolis, MD: Naval Institute Press.
Mainwaring, Henry. 1922. The Life and Works of Sir Henry Manwaring. Edited by G.E Manwaring and W.G. Perrin. Vol. 2. 2 vols. London: THe Navy Records Society.
Olaberria, Juan-Pablo. 2018. Ship Design Knowledge in Early Modern Europe: Royal Yachts and the Shared Knowedge of Ship-designers and Common Shipwrights. Vol. 1. 2 vols. Southampton: Doctoral Dissertation; University of Southampton.
Last edited:
Using the rule of thumb of a trim of 2', or by the current reconstruction with a trim of 1' 10", the swimming line drawn on the diagram above appears grossly out of position, angled far too steeply down at the bow. Has a hull model for the current reconstruction been tests in a hydrotank, with ballast being shifted fore and aft to see the effect on trim?
You certainly don't see the Prince Royal of 1610 having such a steep swimming line when afloat... The drawing seems way off.

You certainly don't see the Prince Royal of 1610 having such a steep swimming line when afloat... The drawing seems way off.

Last edited:
- Joined
- Jun 29, 2024
- Messages
- 1,441
- Points
- 393

Calculating a vessel’s displacement requires knowing two factors; the vessel’s weight and the weight of water displaced by the submerged hull form. For the ship to be in equilibrium these must of course be equal to each other.
The weight displaced by the submerged hull is tedious but not conceptually difficult to calculate. Each body plan section for the hull shape is broken into easily calculated shapes and the area of each shape determined. This area of each body plan sectio can be plotted as a curve of areas vs hull length along the keel and the area under the curve is determined by simple numerical methods such as the trapezoidal rule. The result was then multiplied by the density of water. Even today computerized hydrostatic programs basically use this same methods although possibly with more accurate numerical integration algorithms.
The problem was determining the vessel’s weight. As Ferriero explains shipyard construction practices of the time prevented accurately predicting the weight of the finished ship. This problem persisted into the dawn of iron and steel ship construction, eg; the US Navy’ “light draft” Civil War Monitors.
Predicting the vessel’s trim requires knowing the ship’s center of gravity and center of buoyancy. Both of these are calculated by using moments. This involves multiplying the weight of each construction item by its lever arm from a selected point. The result is summed and divided by the total weight to provide the longitudinal position of the CG. Calculation of the center of buoyancy uses similar methodology. Whether shipwrights of the 1600’s understood this process is unknown but in any case, not knowing weights, let alone their distribution they could not accurately predict trim.
Roger
The weight displaced by the submerged hull is tedious but not conceptually difficult to calculate. Each body plan section for the hull shape is broken into easily calculated shapes and the area of each shape determined. This area of each body plan sectio can be plotted as a curve of areas vs hull length along the keel and the area under the curve is determined by simple numerical methods such as the trapezoidal rule. The result was then multiplied by the density of water. Even today computerized hydrostatic programs basically use this same methods although possibly with more accurate numerical integration algorithms.
The problem was determining the vessel’s weight. As Ferriero explains shipyard construction practices of the time prevented accurately predicting the weight of the finished ship. This problem persisted into the dawn of iron and steel ship construction, eg; the US Navy’ “light draft” Civil War Monitors.
Predicting the vessel’s trim requires knowing the ship’s center of gravity and center of buoyancy. Both of these are calculated by using moments. This involves multiplying the weight of each construction item by its lever arm from a selected point. The result is summed and divided by the total weight to provide the longitudinal position of the CG. Calculation of the center of buoyancy uses similar methodology. Whether shipwrights of the 1600’s understood this process is unknown but in any case, not knowing weights, let alone their distribution they could not accurately predict trim.
Roger
Darvis,
The line in the figure is, indeed, drawn too steeply. I noted that the figure was not drawn to scale because I intended for it only to illustrate that the three relevant points do not fall on it. The important thing is to focus on the trim and the the swimming line's heights at the bow and stern that I wound up using for the current plans. A trim of only 1 foot 10 inches on a drawing that is to scale, it is not all that steep. Imagine set of plans for the Sovereign drawn at 1:48 scale. The line at the bow will be a little less than half an inch lower than it is at the stern. If you're feeling really energetic, you can draw out what I've done using the dimensions for the stem, keel, and post that I have provided, and then draw the swimming line on the result.
And, Roger is certainly correct. Seventeenth shipwrights could not accurately predict trim. As I noted, "estimated swimming line" is probably a better term for what they used. It is clear, though, that they nevertheless attempted to estimate the trim, and that they incorporated their estimates into their plans. As the Treatise's author notes, the decks and the ports are set off from this line. The implication is that they did this despite their errors of estimation.
I also agree with Roger in that you'd have to know the weight to accurately estimate the trim, and figuring out the weights of the Sovereign's timbers is difficult at best.
The line in the figure is, indeed, drawn too steeply. I noted that the figure was not drawn to scale because I intended for it only to illustrate that the three relevant points do not fall on it. The important thing is to focus on the trim and the the swimming line's heights at the bow and stern that I wound up using for the current plans. A trim of only 1 foot 10 inches on a drawing that is to scale, it is not all that steep. Imagine set of plans for the Sovereign drawn at 1:48 scale. The line at the bow will be a little less than half an inch lower than it is at the stern. If you're feeling really energetic, you can draw out what I've done using the dimensions for the stem, keel, and post that I have provided, and then draw the swimming line on the result.
And, Roger is certainly correct. Seventeenth shipwrights could not accurately predict trim. As I noted, "estimated swimming line" is probably a better term for what they used. It is clear, though, that they nevertheless attempted to estimate the trim, and that they incorporated their estimates into their plans. As the Treatise's author notes, the decks and the ports are set off from this line. The implication is that they did this despite their errors of estimation.
I also agree with Roger in that you'd have to know the weight to accurately estimate the trim, and figuring out the weights of the Sovereign's timbers is difficult at best.
The drawing was described as out of scale, but it appears to be correct in proportion. So, I believed that the points chosen were meant to be fairly accurate. Thanks for the clarification. I will take your advise and mount my model at a slight aft trim as if it were afloat. Great idea. Thanks for all the information you provide in this thread. Truly a valuable resource!Darvis,
The line in the figure is, indeed, drawn too steeply. I noted that the figure was not drawn to scale because I intended for it only to illustrate that the three relevant points do not fall on it. The important thing is to focus on the trim and the the swimming line's heights at the bow and stern that I wound up using for the current plans. A trim of only 1 foot 10 inches on a drawing that is to scale, it is not all that steep. Imagine set of plans for the Sovereign drawn at 1:48 scale. The line at the bow will be a little less than half an inch lower than it is at the stern. If you're feeling really energetic, you can draw out what I've done using the dimensions for the stem, keel, and post that I have provided, and then draw the swimming line on the result.
And, Roger is certainly correct. Seventeenth shipwrights could not accurately predict trim. As I noted, "estimated swimming line" is probably a better term for what they used. It is clear, though, that they nevertheless attempted to estimate the trim, and that they incorporated their estimates into their plans. As the Treatise's author notes, the decks and the ports are set off from this line. The implication is that they did this despite their errors of estimation.
I also agree with Roger in that you'd have to know the weight to accurately estimate the trim, and figuring out the weights of the Sovereign's timbers is difficult at best.
Section IV: The Sheer Plan (continued)
The Number and Spacing of the Sovereign’s Bends
Overview
The previous section took the first step towards drawing the decks by determining the swimming line’s location. We need one more step, though, before we can draw them. We need to find where the lower gun deck’s fore and aft ends are. This, in conjunction with the swimming line, allows us to determine its entire course, and the courses of most of the other decks.Determining the lower gun deck’s length and course is further assisted by finding how the bends along the Sovereign were spaced. As stated earlier, a “bend” is every third or fourth of a ship’s frames. They are what shipwrights drew bends on their plans instead of frames.
The Treatise’s Method
The Treatise tells us that we are to separately find the number of bends fore and aft of the midship bend. We are to find the former number by first finding the distance between the stem’s inner rake and the midship bend. This equals ⅓ of the keel’s length plus the stem’s inner rake, which is 60 feet on the Treatise’s ship. We then divide this by the bends’ spacing. The spacing is not fixed. The Treatise’s author notes that we could either divide the 60-foot distance into 24 spaces that are 2 ½ feet apart, or into 20 spaces that are 3 feet apart. He chose the latter.We are to find the number of bends aft of the midship bend by adding the sternpost’s rake to ⅔ of the keel’s length (which is where the midship bend is) by the spacing between bends. The spacing between the aft bends need not be the same as that between the fore bends. The spacing between the aft bends on the Treatise’s ship is 2 ½ feet, or 30 inches. Shipwrights required the number of fore and aft bends to each be an integer (for example, there cannot be 32 ¾ fore or aft bends because this number contains a fraction). Adjustments were made to ensure this. The Treatise’s author reduced his inner stem rake by 2 inches to do so. Integers were preferred because they eliminated the need to work with decimals or fractions in subsequent calculations.
The Sovereign of the Seas
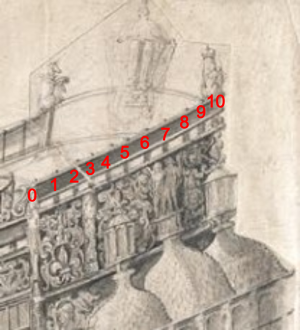
We can characterize the Sovereign’s bends by using the Pett painting. It shows them as vertical timbers that run along the top of the forecastle, the half and quarter decks, and roundhouse (because I cannot show the Pett painting, I will illustrate the point using van de Velde. The bends he shows along the Sovereign’s roundhouse are numbered in red in Figure 24).[1] The Pett painting also shows that all of bends are equally spaced[2], and that that their centers are separated by a distance equal to the size of the gun ports on the middle gun deck. Phineas Pett tells us that this is 30 inches, which is the same as the spacing of the aft bends of the Treatise’s ship. [3]This spacing produces 37.07 bends aft of the midship bend (I obtained this as described by the Treatise). A shipwright would likely have rounded this to 37 bends. The spacing also produces 32.13 fore bends, which I obtained by adding Pett’s stated stem rake (38 feet) to ⅓ of the keel’s length.[4] A shipwright would likely have rounded this number, too. Modern spreadsheets remove concerns about confining the total number of bends to integers so I have not rounded any bend numbers when computing the courses of the rising and narrowing lines (these lines will be described in later sections).[5]
Figure 24. Van de Velde’s Portrayal of the Tops of the Sovereign’s Bends
Note: The bends are the vertical timbers that are under the red numbers. The bends along the entire ship are better described by the Pett painting, but restrictions on cropping and labelling it prevent me from showing it.
Having found the number of the Sovereign’s bends, we need to number them. Numbering is important because many of the calculations we will perform later use the bend’s number. The bends should be assigned consecutively increasing numbers as they move away from the midship bend. Thus, the midship bend is bend “0”,[6] the bends immediately fore and aft of it are both numbered as “1”, the adjacent fore and aft bends “2”, and so on. I continue the numbering beyond the stem and the sternpost to help locate the taffrail and to determine the beakhead’s length.
I dispense with the usual system of identifying the bends using letters or symbols because doing so is cumbersome for a ship with as many bends as the Sovereign had. Further, the computations that locate the rising lines and tell us how this ship narrows use each bend’s number. It is simpler to consistently refer to bends this way instead of switching between numbers and letters or symbols.
References
Endsor, Richard. 2020. The Master Shipwright's Secrets. New York: Osprey Publishing.[1] Endsor has done something similar when interpreting a drawing of the Tyger by van de Velde. The bends in his relevant drawing appear between the gunwale and plank sheer of the ship’s forecastle. (Endsor 2020, 174) One can argue that the Pett painting is different because it shows vertical timbers that support the upper railings. Even if this is the case, their position and spacing yields the same results.
[2] We cannot see any bends along the waist. I am deferring discussion of the number of bends here until the weather deck’s lengths are discussed.
[3] In practice, determining the spacing between bends involves more than just comparing the distance between bends to the size of a gun port. It also involves testing other possible spacings to ensure that we are using one that produces a ship whose total length, as computed from the bends (which is the number of bends shown on the Pett painting times the space between bends), is as close as possible to the total length we obtain by summing the post’s rake, the keel’s length, and the stem’s rake (all of which are given by Pett). It ais also necessary to ensure that the masts, whose positions are fixed, are at appropriate places. For example, if we choose spacing that is extremely small, the mizzen will wind up on the roundhouse, which is clearly incorrect. Similarly, if we choose spacing that is extremely large, the mizzen will wind up at the very fore end of the quarter deck, or even on the half deck, which is also clearly incorrect.
[4] We obtain nearly identical results if we follow the Treatise. Adding the stem’s inner rake to ⅓ of the keel’s length yields 32.09 bends fore of the midship bend. A shipwright would have rounded this to 32 bends.
[5] Although the amount of rounding is likely too small to have concerned 17th shipwrights, deciding whether to round illustrates one of the trade-offs one encounters when trying to reconstruct the Sovereign. For example, the rounded number of aft bends is about ¾ of an inch shorter than the sum of ⅔ the keel plus Pett’s rake of the post. Therefore, rounding reduces the keel’s length or the post’s rake by this amount. This makes one of these dimensions shorter than Pett specifies. On the other hand, if we do not round, we retain the proper lengths, but are likely computing the courses of our rising and narrowing lines slightly differently than these shipwrights would have done.
[6] In reality, there is no need to number the midship bend at all. I have done so to simplify the numbering’s explanation.
Since the bends are separated by 30 inches, 0.17 bends = 0.17 X 30 = 5.10 inches.
What I am doing is not all that strange. The Treatise's author also encountered bends that were not integers, so he rounded them. It's important to understand that some of these early works were written by mathematicians (the Treatise is an example). Their calculations were heavily mathematical, at least for their time. This will become apparent when we talk about how the Treatise's author calculated his rising and narrowing lines. He used cosines, versed sines, and more.
What I am doing is not all that strange. The Treatise's author also encountered bends that were not integers, so he rounded them. It's important to understand that some of these early works were written by mathematicians (the Treatise is an example). Their calculations were heavily mathematical, at least for their time. This will become apparent when we talk about how the Treatise's author calculated his rising and narrowing lines. He used cosines, versed sines, and more.
- Joined
- Jun 4, 2024
- Messages
- 62
- Points
- 68

Hi Bela;
Charlie's point here is that dividing the calculated overall length of the ship by 30" does not give a whole number (integer) as an answer, because the overall length is not divisible by 30. There is therefore a need to round up or down to get rid of the remainder. Once this has been done, the designer is working only with whole numbers.
The 0.17 (actually Charlie gives 0.07) bends is neither needed, nor desired, and occurs only in the preliminary stages of calculations.
Ratty
Charlie's point here is that dividing the calculated overall length of the ship by 30" does not give a whole number (integer) as an answer, because the overall length is not divisible by 30. There is therefore a need to round up or down to get rid of the remainder. Once this has been done, the designer is working only with whole numbers.
The 0.17 (actually Charlie gives 0.07) bends is neither needed, nor desired, and occurs only in the preliminary stages of calculations.
Ratty